Função Quadrática - CN/EPCAR
3 participantes
Página 1 de 1
Função Quadrática - CN/EPCAR
por castelo_hsi Sáb 27 Nov 2021, 14:55
Na figura são representadas as parábolas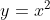 
e 
. Considere os segmentos verticais que tem uma extremidade em cada uma das parábolas. O menor desses segmentos mede:
a) 5/2
b) 3/2
c) 2
d) 3
e) 4
*Não tenho o gabarito
a) 5/2
b) 3/2
c) 2
d) 3
e) 4
*Não tenho o gabarito
Última edição por castelo_hsi em Sáb 27 Nov 2021, 15:37, editado 1 vez(es)
castelo_hsi- Mestre Jedi
- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
Rory Gilmore gosta desta mensagem
Re: Função Quadrática - CN/EPCAR
por tales amaral Sáb 27 Nov 2021, 15:14
Se [latex]f(x) = x^2[/latex] e [latex]g(x) = -x^2+2x-3[/latex], temos que o comprimento dos segmentos é dado pela distância entre os pontos [latex]A = (x,f(x))[/latex] e [latex]B = (x,g(x))[/latex]:
[latex]\begin{align*} d(A,B) &= \sqrt{\left[ f(x)-g(x)\right ]^2 + (x-x)^2}\\~\\ &= \sqrt{\left(x^2 +x^2-2x+3 \right )^2}\\~\\ &= | 2x^2 -2x+3 | \\~\\ &= \left|\left(\sqrt{2}x\right)^2 - 2\cdot \sqrt{2} \cdot \dfrac{1}{\sqrt{2}}\cdot x + \left(\dfrac{1}{\sqrt{2}} \right )^2+\dfrac{5}{2}\right|\\~\\ &= \left|\left( \sqrt{2}x - \dfrac{1}{\sqrt{2}}\right )^2+\dfrac{5}{2}\right| \end{align*}[/latex]
Temos que a menor distância é [latex]\dfrac{5}{2}[/latex].
[latex]\begin{align*} d(A,B) &= \sqrt{\left[ f(x)-g(x)\right ]^2 + (x-x)^2}\\~\\ &= \sqrt{\left(x^2 +x^2-2x+3 \right )^2}\\~\\ &= | 2x^2 -2x+3 | \\~\\ &= \left|\left(\sqrt{2}x\right)^2 - 2\cdot \sqrt{2} \cdot \dfrac{1}{\sqrt{2}}\cdot x + \left(\dfrac{1}{\sqrt{2}} \right )^2+\dfrac{5}{2}\right|\\~\\ &= \left|\left( \sqrt{2}x - \dfrac{1}{\sqrt{2}}\right )^2+\dfrac{5}{2}\right| \end{align*}[/latex]
Temos que a menor distância é [latex]\dfrac{5}{2}[/latex].
tales amaral- Monitor
- Mensagens : 579
Data de inscrição : 02/05/2020
Idade : 20
Localização : Serra, ES -
Rory Gilmore e castelo_hsi gostam desta mensagem
castelo_hsi- Mestre Jedi
- Mensagens : 625
Data de inscrição : 27/06/2021
Localização : São Paulo - SP
Rory Gilmore e tales amaral gostam desta mensagem
Re: Função Quadrática - CN/EPCAR
por Rory Gilmore Sáb 27 Nov 2021, 15:48
Tales fez tudo correto, porém de forma MUITO TRABALHOSA. Então, para simplificar os cálculos vou deixar uma sugestão:
A distância entre dois pontos é mínima se o seu quadrado for mínimo. Daí, eliminamos a necessidade de usar a raiz:
d(A, B)² = (2x² - 2x + 3)²
Queremos d² mínimo, então basta calcular o mínimo de x² - 2x + 3 que ocorre para x = 1/2.
Substituindo x = 1/2 na fórmula da distância obtemos d = 5/2.
A distância entre dois pontos é mínima se o seu quadrado for mínimo. Daí, eliminamos a necessidade de usar a raiz:
d(A, B)² = (2x² - 2x + 3)²
Queremos d² mínimo, então basta calcular o mínimo de x² - 2x + 3 que ocorre para x = 1/2.
Substituindo x = 1/2 na fórmula da distância obtemos d = 5/2.
Rory Gilmore- Monitor
- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
tales amaral e castelo_hsi gostam desta mensagem
Tópicos semelhantes» Função Quadrática EPCAR 2022
» (EPCAR 2004) Função afim e quadrática
» Função quadrática e área máxima - EPCAR/CN
» Inequação quadrática - função quadrática
» Descobrir função inversa de uma função quadrática
» (EPCAR 2004) Função afim e quadrática
» Função quadrática e área máxima - EPCAR/CN
» Inequação quadrática - função quadrática
» Descobrir função inversa de uma função quadrática
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
