Expressão Trigonométrica.

Calcule a seguinte expressão:

2.sen(17.x) + √3.cos(5.x) + sen(5.x) = 0

Resp.: Sem gabarito


Bom dia colegas!
Tentei resolver tal equação abrindo o sen.(17x)... para tentar achar alguma relação com os sen.(5x) e o cos.(5x)... porém, sem sucesso

Obrigado! :D

Olá Floral Fury;

Batendo o olho vejo apenas uma solução trivial, onde:



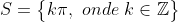
Testando, para k = 0:



Fica em aberto para quem quiser desenvolver!

Existe uma incoerência entre o enunciado e sua tentativa: você fala em cos(5.x) e no enunciado isto não aparece. Vou supor que o último termo seja cos(5.x)

2.sen(17.x) + √3.sen(5.x) + cos(5.x) = 0

√3.sen(5.x) + cos(5.x) = 2.[(√3/2).sen.(5x) + (1/2).cos(5.x)] =

= 2.[cos30º.sen(5x) + sen30º.cos(5.x)] = 2.sen(5.x + 60º)

2.sen(17.x) + 2.sen(5.x + 60º) = 0 --> 2.{sen(17.x) + sen(5.x + 60º)} = 0

Usando prostaférese:

2.{sen(17.x) + sen(5.x + 60º)} = 0 --->

2.2.sen{[17.x + (5.x + 60º)]/2}.cos{17.x - (5.x + 60º)]/2} = 0

4.sen(11.x + 30º).cos(6.x - 30º) = 0 ---> Complete

Perdão amigos, o certo é o cos.(5x) ao lado do √3

Isso altera em algo a sua resolução, Elcio?
Irei completar mais tarde, e dps mando aqui para vcs verem!

Peço perdão, novamente... E agradeço!!

Não altera: eu já usei cos(5.x)

Novamente, obrigado pela ajuda, mais uma vez!
E perdão pelo equívoco!

Obrigado amigos!

Elcio...

O valor não é alterado não? Pois o cos(5x) está ligado ao √3
Logo ficaria, trocando as ordens:

2 . [(√3/2).cos(5x) + (1/2)sen(5x)]
2 . [cos.30 . cos(5x) + sen.30 . sen(5x)]
2 . [cos.(30 - 5x)]

Não ficaria assim?

Eu entendi errado: achei que cos(5.x) fosse o termo sozinho.
Isto vai alterar sim, conforme vc mostrou
Complete e poste por favor.

Ok, sem problemas!!  


Então, refazendo para o senhor ver:

 2 sen(17x) + √3 . cos(5x) + sen(5x) = 0
                     2/2 . [ √3 . cos(5x) + sen(5x) ]
                     2 . [ (√3/2) . cos(5x) + (1/2) . sen(5x) ]
                     2 . [ cos.30º . cos(5x) + sen.30º . sen(5x) ]
                     2 . cos(30 - 5x)
 2 sen(17x) + 2 cos(30 - 5x) = 0
 2 [ sen(17x) + cos(30 - 5x) ] = 0
 [ sen(17x) + cos(30 - 5x) ] = 0

Agora não dá mais para aplicar prostaférese....
Entretanto, percebi que é possível assumir que o ângulo não é 30º, mas sim 60º

O que o senhor acha?

Segue a resolução para o senhor ver quando assumimos o ângulo como 60º ao invés de 30º:

√3 cos.(5x) + sen(5x) = 0
2.2 [ √3 cos(5x) + sen(5x) ] = 0
2 . { [ (√3/2) cos.(5x) + (1/2) sen.(5x) ] } = 0
2 . [ sen.60º . cos(5x) + cos.60º . sen(5x) ] = 0
2 . sen(60 + 5x) = 0
----------------

2.sen(17x) + 2.sen(60 + 5x) = 0
2 [ sen(17x) + sen(60 + 5x) ] = 0
2 . { 2.sen[(17x + (60 + 5x))/2].cos[(17x - (60 + 5x))/2] } = 0
4.sen[(22x + 60)/2].cos[(12x - 60)/2] = 0
4.sen(11x + 30).cos(6x - 30) = 0
sen(11x + 30).cos(6x - 30) = 0

Aí então temos que:
 sen(11x + 30) = 0 -----> 11x + 30 = k.π
                                                   x = (k.π - 30)/11
 cos.(6x - 30) = 0 ------> 6x - 30 = k.π/2
                                               x = (kπ + 60)/12

Obrigado pela ajuda que me foi dada nesse tópico!!
Perdão a postagem excessiva de mensagens tbm kkkkkk
Creio que seja isso... caso cometi algum erro, não há problema nenhum em este ser pontuado!

Obrigado!