Retângulo inscrito em um círculo

por **alansilva** Sex 05 Fev 2021, 18:42

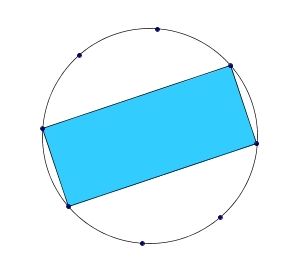
Um círculo de raio 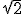$Retângulo inscrito em um círculo Mimetex_$ está dividido em 8 partes iguais, como mostra a figura. A área do retângulo assinalado é:

a) $Retângulo inscrito em um círculo Mimetex_$ b) $Retângulo inscrito em um círculo Mimetex_$ c) $Retângulo inscrito em um círculo Mimetex_$ d) $Retângulo inscrito em um círculo Mimetex_$ e) NRA.

Gabarito: C

por **Elcioschin** Sex 05 Fev 2021, 19:03

Retângulo inscrito em um círculo Retins11

Outro modo maio fácil e rápido:

Trace trapézio acima do diâmetro, formando por 3 lados h:

L = h.cos45º + h + h.cos45º ---> L = h.(√2 + 1)

L² + h² = (2.r)² ---> L² + h² =(2.√2)² --> L² + h² = 8

Resolva o sistema e calcule L, h

por **Giovana Martins** Sex 05 Fev 2021, 19:35

Acredito que pelo Teorema das Áreas a questão saia facilmente também.

Aproveitando a figura do Élcio.

[latex]\\\mathrm{A=2\left [ \frac{1}{2}absen(\theta)+\frac{1}{2}absen(3\theta ) \right ],com\ a=b=R}\\\\\mathrm{A=R^2[sen(\theta )+sen(3\theta)],com\ \theta =\frac{360^{\circ}}{8}=45^{\circ}}\\\\\mathrm{A=\left ( \sqrt{2} \right )^2\left [ sen(45^{\circ})+sen(135^{\circ}) \right ]=2\sqrt{2}}[/latex]

Nota: esta minha resolução bateu com a primeira resolução do Élcio, porém não bateu com a segunda. A propósito, nenhuma das resolução batem com o gabarito hahahaha. Não sei se eu errei algo, mas você tem certeza que o gabarito é este, Alan?

por **Medeiros** Sex 05 Fev 2021, 21:45

o gabarito está errado. Sobrou a alternativa ridícula, ie., NRA.

1)
a área de um quadrilátero qualquer, conhecidas suas duas diagonais e o ângulo entre elas, pode ser calculada como se fosse a do triângulo cujos lados são essas diagonais.

Retângulo inscrito em um círculo Scre1176

2)
as duas diagonais de um retângulo o dividem em quatro triângulos de mesma área.

Retângulo inscrito em um círculo Scre1177

por **alansilva** Sex 05 Fev 2021, 22:12

Giovana, esta questão é do livro Geometria II do Morgado. Com certteza gabarito está errado. Obrigado a você, Medeiros e o Élcio

por **Giovana Martins** Sex 05 Fev 2021, 22:14

De nada, Alan!

por **Medeiros** Sex 05 Fev 2021, 23:31

Olá, Alan.

Esta não é a primeira rata do livro do Morgado que vejo aqui no fórum. Acho que quem fez a revisão do livro (dos moldes para impressão) comeu muita mosca.

por **Elcioschin** Sáb 06 Fev 2021, 09:55

Giovana

A minha 2ª solução também bate com a solução S = 2.√2:

L = h.(√2 + 1) ---> L² = h².(3 + 2.√2) ---> I

L² + h² = (2.r)² --> h².(3 + 2.√2) + h² = 8 ---> h².(4 + 2.√2) = 8 ---> h² = 4 - 2.√2 ---> II

I) L² = (4 - 2.√2).(3 + 2.√2) ---> L² = 4 + 2.√2 --> III

S² = L².h² ---> S² = (4 + 2.√2).(4 - 2.√2) ---> S² = 8 ---> S = 2.√2

por **raimundo pereira** Sáb 06 Fev 2021, 14:52

por **Medeiros** Sáb 06 Fev 2021, 16:13

Raimundo

você multiplicou a hipotenusa pelo cateto e diz que isso é a área do triângulo retângulo (metade do quadrilátero)?

também não consegui a resposta indicada na conta.