Círculo inscrito em um triângulo retângulo

por RatinhoPequenino Sex 06 maio 2022, 11:14

(FEI-SP) O diâmetro de um círculo inscrito em um triângulo retângulo de hipotenusa 5 cm e catetos 3 cm e 4 cm mede:

A) 1 cm
B) √ 2cm
C) 2 cm
D) 2√ 2 cm
E) 4 cm

por DGL72021 Sex 06 maio 2022, 12:28

O raio de uma circunferência inscrita em um triângulo retângulo é a subtração do semiperímetro do triângulo pela hipotenusa, logo:

2p=5+3+4--->p=6

raio= semiperímetro - hipotenusa

r=6-5
r=1
diâmetro é 2 vezes o raio, logo: 2.r----> 2.1

d=2 cm

por RatinhoPequenino Sex 06 maio 2022, 13:21

DGL72021 escreveu:O raio de uma circunferência inscrita em um triângulo retângulo é a subtração do semiperímetro do triângulo pela hipotenusa, logo:

2p=5+3+4--->p=6

raio= semiperímetro - hipotenusa

r=6-5
r=1
diâmetro é 2 vezes o raio, logo: 2.r----> 2.1

d=2 cm

Muito obrigado! Eu não conhecia esse conceito.

Pode demonstrar?

por Ana Laura Guimarães Sex 06 maio 2022, 16:50

RatinhoPequenino escreveu:
DGL72021 escreveu:O raio de uma circunferência inscrita em um triângulo retângulo é a subtração do semiperímetro do triângulo pela hipotenusa, logo:

2p=5+3+4--->p=6

raio= semiperímetro - hipotenusa

r=6-5
r=1
diâmetro é 2 vezes o raio, logo: 2.r----> 2.1

d=2 cm

Muito obrigado! Eu não conhecia esse conceito.

Pode demonstrar?

Círculo inscrito em um triângulo retângulo R.5db30cc246704f5d302156d5a154ab3d?rik=kgUcJStbixgg2A&riu=http%3a%2f%2f2.bp.blogspot.com%2f-UuwwHRJyr58%2fTrqltWuYFhI%2fAAAAAAAAB9g%2fKd-SxD_l5eY%2fw1200-h630-p-nu%2fdemo

por DGL72021 Sex 06 maio 2022, 17:14

Vamos lá,

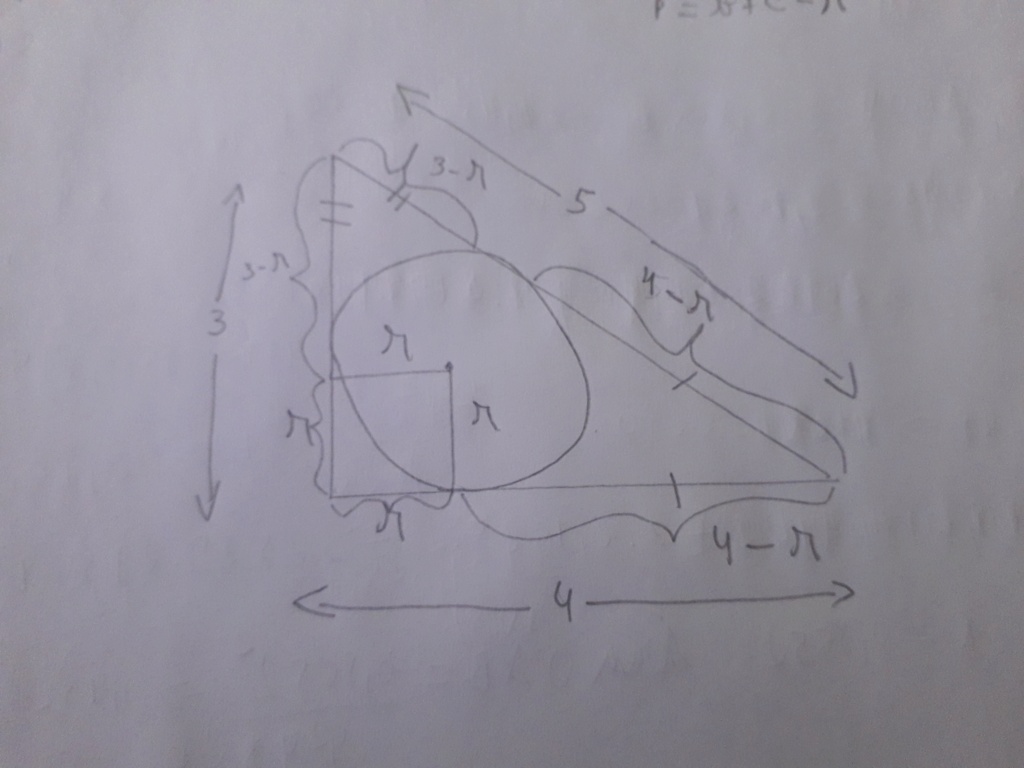
Círculo inscrito em um triângulo retângulo 20220510

Observe que tangentes do mesmo ponto tem o mesmo comprimento(indiquei na figura com traços no triângulo /=4-r e dois traços //=3-r ).

Perímetro=3-r+r+4-r+r+3-r+4-r
12=7+7-2r----->12-14=-2r
r=1

5=a 3=b 4=c semiperímetro=p raio=r

r=p-a ∵ 2p=b-r+r+c-r+r+a----->2p=b+c+a------>2p=b+c+b-r+c-r------>2p=2b+2c-2r----->p=(b+c-r).2/2
p=b+c-r

substituindo o p na primeira fórmula:
r=b+c-r-a
2r=b+c-a
r=(b+c-a)/2