FUVEST 2017: B→ resultante no centro de um quadrado

As figuras representam arranjos de fios longos, retilíneos, paralelos e percorridos por correntes elétricas de mesma intensidade. Os fios estão orientados perpendicularmente ao plano desta página e dispostos segundo os vértices de um quadrado. A única diferença entre os arranjos está no sentido das correntes: os fios são percorridos por correntes que entram  ou saem  do plano da página.


O campo magnético total é nulo no centro do quadrado apenas em:
a)  I
b) II
c)  I e II
d) II e III
e) III e IV


Minha resolução:


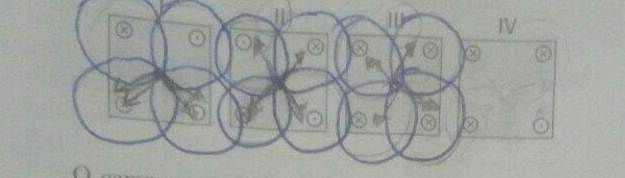
Alguém consegue resolver de uma forma mais rápida do que essa de traçar as linhas de campo magnético no centro pra tirar os vetores de indução magnética?

Outro ponto:
Ao pesquisar outras formas de resolução, encontrei que dá pra calcular, por exemplo, o valor do vetor de indução magnética  resultante (|Br|) no quadrado I em função de |B|:




|Br| = 2.|B| . √2

Alguém pode me elucidar sobre a presença da '√2' ?

Você não precisa calcular cada campo B no centro, pois o módulo de todos eles são iguais (esqueça √2) e nem precisa calcular a resultante dos quatro campos

O que importa é que os 4 vetores tem ser opostos 2 a 2

A sua última figura para I está correta: é óbvio que a resultante não é nula e aponta para baixo.

Complete

Sobre a forma de resolução, creio que seja isso mesmo, não sei se seria muito efetivo decorar as situações em que o campo é nulo.

Com relação ao √2, você precisa fazer a soma dos vetores de indução. Sendo B o campo magnético gerado pelo fio, têm-se um triângulo retângulo de catetos 2B. 

Utilizando o teorema de Pitágoras, o vetor resultante é 2√2B

(2B)² + (2B)² = B_R²
Br = 2√2B