questão 50 cap 2 Problemas sem problemas vol 2

por Lima015 Dom 10 maio 2020, 05:46

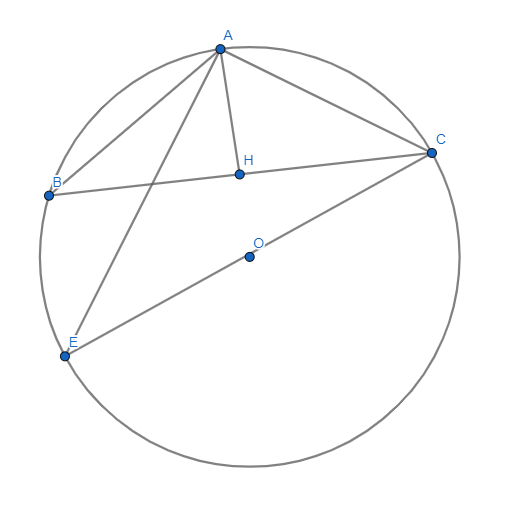
AB=10cm e AC=12cm são dois lados de um triangulo ABC, inscrito em um circulo. Sabendo que a altura AH relativa ao lado BC e igual a 4 cm, calcular o valor do raio deste circulo.

por **Rory Gilmore** Dom 10 maio 2020, 12:22

O ∆AHB é semelhante ao ∆CEA.

AB/2R = AH/AC
10/2R = 4/12
5/R = 2/6
2.R = 30
R = 15 cm

questão 50 cap 2 Problemas sem problemas vol 2 Sem_tz69

por **Mateus Meireles** Dom 10 maio 2020, 13:04

Olá, Lima015.

Outra solução:

A área de qualquer triângulo inscrito em uma circunferência é S = abc/4R, em que a, b e c são os lados do triângulo e R o raio da circunferência.

(10)*(12)*(BC)/4R = (BC)*4/2

R = 15 cm.

Abs.