questão 57 cap 2 Problemas sem problemas vol 2

por Lima015 Dom 10 maio 2020, 06:11

Na figura abaixo, tem-se um trapézio ABCD com bases de 10 cm e 15 cm. EF é uma paralela às bases passando pelo ponto de encontro das diagonais.Calcular a medida do segmentos EF.

*consegui descobri que é a média harmonica, mas não sei o porque.Se alguém souber ou tiver outra resolução....

por **Elcioschin** Dom 10 maio 2020, 13:21

O trapézio é qualquer. Para facilitar a solução, por GA vou considerar um trapézio retângulo:

questão 57 cap 2 Problemas sem problemas vol 2 Trap_e10

por **Medeiros** Seg 11 maio 2020, 02:49

Lima,

se você conseguiu resolver mas não sabe o porquê, devia ter mostrado suas contas.
Em todo o caso, vai lá a explicação do porquê é a média harmônica.

questão 57 cap 2 Problemas sem problemas vol 2 Scree692

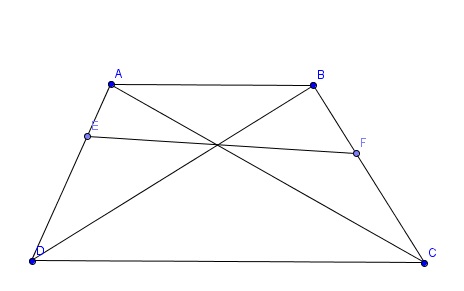
esqueci de completar a conta: FE = 12

e deixando mais claro a média,

\\\frac{1}{p}= \frac{1}{q} = \frac{1}{10} + \frac{1}{15}

ou

\\FE = \frac{2}{\frac{1}{10} + \frac{1}{15}} \;\;\;\text{......... media harmonica}

este tipo de fórmula já foi exaustivamente abordado, inclusive com um exemplo deste tipo, no tópico 'linkado' abaixo. Infelizmente muitas figuras de resoluções não mais estão disponíveis.
https://pir2.forumeiros.com/t118203-formula-importante