Geometria Plana triangulos
4 participantes
Página 1 de 1
 Geometria Plana triangulos
Geometria Plana triangulos
Dado um triângulo qualquer ABC e uma reta “r” exterior ao mesmo e sabendo que as
distâncias de seus vértices à essa reta são 4cm, 8cm e 3cm, calcular a distância do
baricentro à mesma reta.
GAB: 5
distâncias de seus vértices à essa reta são 4cm, 8cm e 3cm, calcular a distância do
baricentro à mesma reta.
GAB: 5
Lima015- Padawan

- Mensagens : 91
Data de inscrição : 29/03/2020
 Re: Geometria Plana triangulos
Re: Geometria Plana triangulos
suponha que essas distâncias dadas sejam as ordenadas (eixo y) dos vértices do triângulo.
ora, o yG é a média aritmética das ordenadas; portanto a distância pedida é:
yG = d = (4 + 8 + 3)/3 = 5
ora, o yG é a média aritmética das ordenadas; portanto a distância pedida é:
yG = d = (4 + 8 + 3)/3 = 5

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR

Elcioschin- Grande Mestre

- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
 Re: Geometria Plana triangulos
Re: Geometria Plana triangulos
como você conseguiu chegar a conclusão que é a média aritmética? É alguma teoria?
Lima015- Padawan

- Mensagens : 91
Data de inscrição : 29/03/2020
 Re: Geometria Plana triangulos
Re: Geometria Plana triangulos
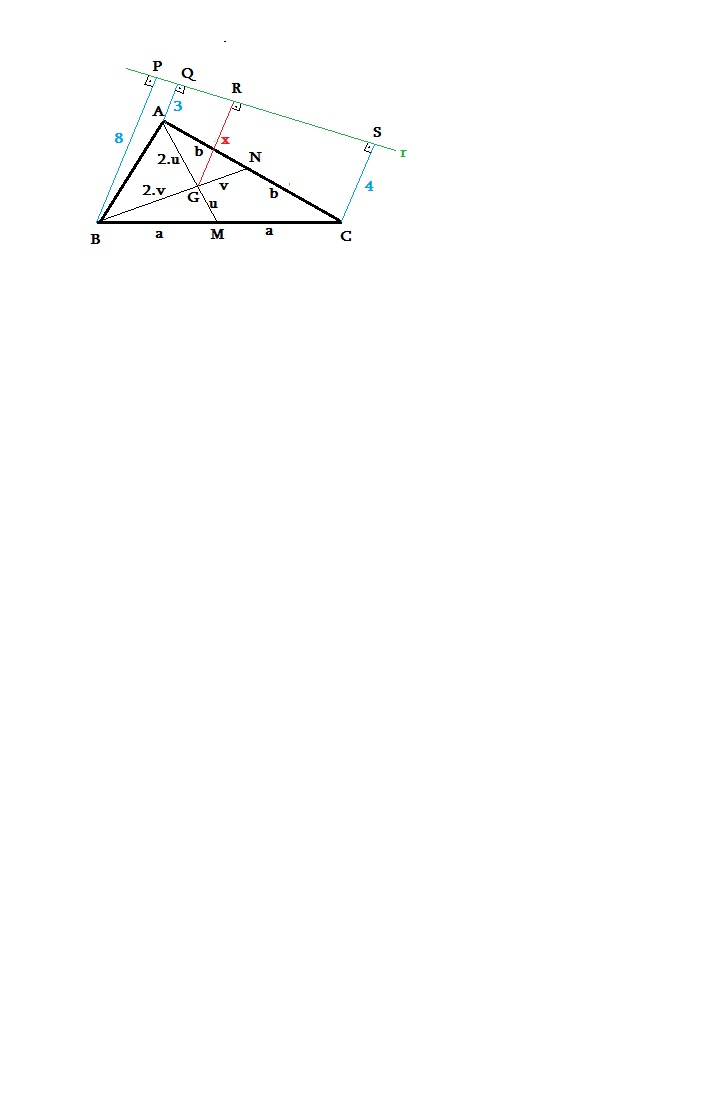
Seja o triângulo ABC de baricentro G, e as distâncias dos vértices A, B e C até a reta r são a, b e c respectivamente. Seja d a distância procurada.
I) M é o ponto médio de AC.
II) MR é base média do trapézio ACHN:
MR = (a + c)/2
III) Vamos destacar agora o trapézio BMRF. BM é mediana de ABC e G é o baricentro, logo BG = 2.GM. Isso nos permite traçar a ST // MR pelo ponto médio de BG.
ST é base média do trapézio BGJF:
ST = (b + d)/2
IV) d é base média do trapézio SMRT:
d = (ST + MR)/2
2.d = ST + MR
2.d = (a + c + b + d)/2
4.d = a + b + c + d
3.d = a + b + c
d = (a + b + c)/3
Portanto d é a média aritmética da soma das distâncias dos vértices até a reta r:
d = (3 + 4 + /3
/3
d = 15/3
d = 5
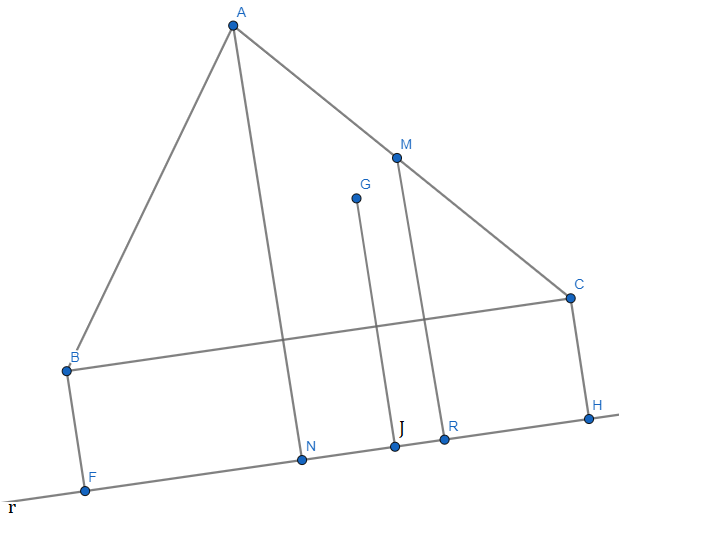
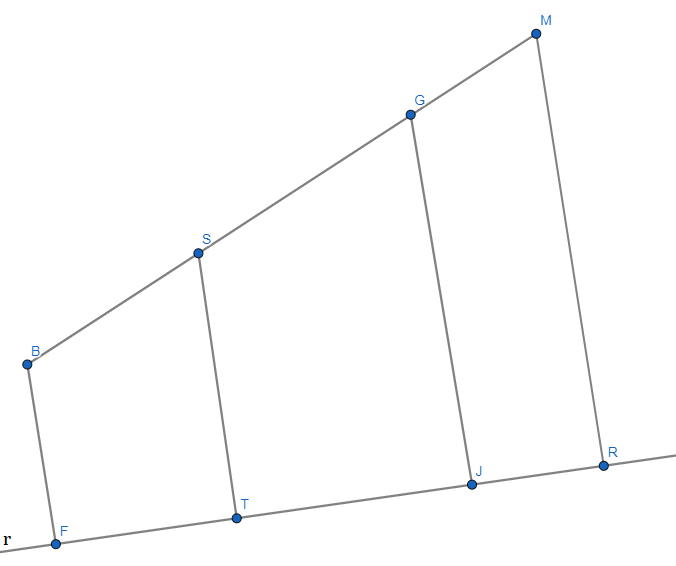
I) M é o ponto médio de AC.
II) MR é base média do trapézio ACHN:
MR = (a + c)/2
III) Vamos destacar agora o trapézio BMRF. BM é mediana de ABC e G é o baricentro, logo BG = 2.GM. Isso nos permite traçar a ST // MR pelo ponto médio de BG.
ST é base média do trapézio BGJF:
ST = (b + d)/2
IV) d é base média do trapézio SMRT:
d = (ST + MR)/2
2.d = ST + MR
2.d = (a + c + b + d)/2
4.d = a + b + c + d
3.d = a + b + c
d = (a + b + c)/3
Portanto d é a média aritmética da soma das distâncias dos vértices até a reta r:
d = (3 + 4 +
d = 15/3
d = 5


Rory Gilmore- Monitor

- Mensagens : 1878
Data de inscrição : 28/05/2019
Localização : Yale University - New Haven, Connecticut
 Re: Geometria Plana triangulos
Re: Geometria Plana triangulos
Não. É calculo; mas é tão intuitivo que nem mostrei.Lima015 escreveu:como você conseguiu chegar a conclusão que é a média aritmética? É alguma teoria?
Lembro que já respondi esta questão no fórum -- devem fazer uns dez anos -- mas agora não encontrei. Segue nova resposta, apesar de que a Rory já elucidou muito bem.
Como tudo o que nos interessa é a distância em relação a reta r, podemos trabalhar apenas com uma dimensão e para nos facilitar a visualização imaginamos um eixo y perpendicular à reta dada.
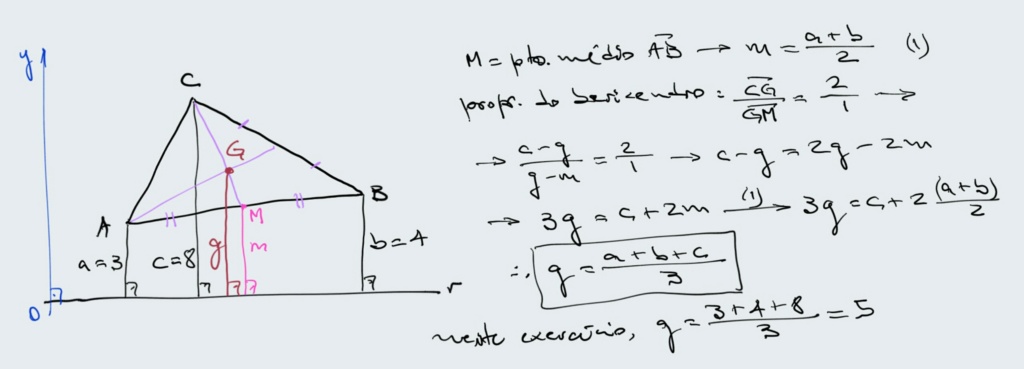
OBS: nesta resolução há um detalhe ao fundo que não foi explicitado, na passagem da segunda para a terceira linha.
A propriedade do baricentro usada refere-se e vale para o segmento CM que, contudo não é perpendicular à reta R. Na verdade o que fizemos aqui foi aplicar o teor. de Tales e, assim, transferir essa proporção (2 : 1) a uma reta (não desenhada) perpendicular à r.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» Geometria Plana: triangulos
» Geometria Plana - Triângulos
» Geometria Plana; Triângulos
» Geometria Plana / Triângulos
» Geometria Plana - Triângulos
» Geometria Plana - Triângulos
» Geometria Plana; Triângulos
» Geometria Plana / Triângulos
» Geometria Plana - Triângulos
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos