ANPAD

ANPAD - Considere as retas r e s do plano cartesiano, definidas pelas seguintes equações
r: 5x + 11y = 29
s: x = -3
Para k∈IR*+, considere a circunferência Ck, definida pela equação x² + y² = k².
Sabe-se que há apenas dois valores de k, representados por k1 e k2, para os quais a circunferência Ck intercepta o conjunto r U s em apenas três pontos.
Qual é o valor da soma k1 + k2?

a) 9
b) 8
c) 5
d) 3
e) 1

Esse problema fica bem difícil de enxergar sem desenhar as retas no plano cartesiano, localizar o centro do círculo (no caso a origem) e analisar as possibilidades. Após desenhar, você vai ver que de fato só existem duas situações em que a circunferência tangenciará as retas em 3 pontos.

Em uma situação, a circunferência será tangente a reta vertical x = -3 dessa maneira:


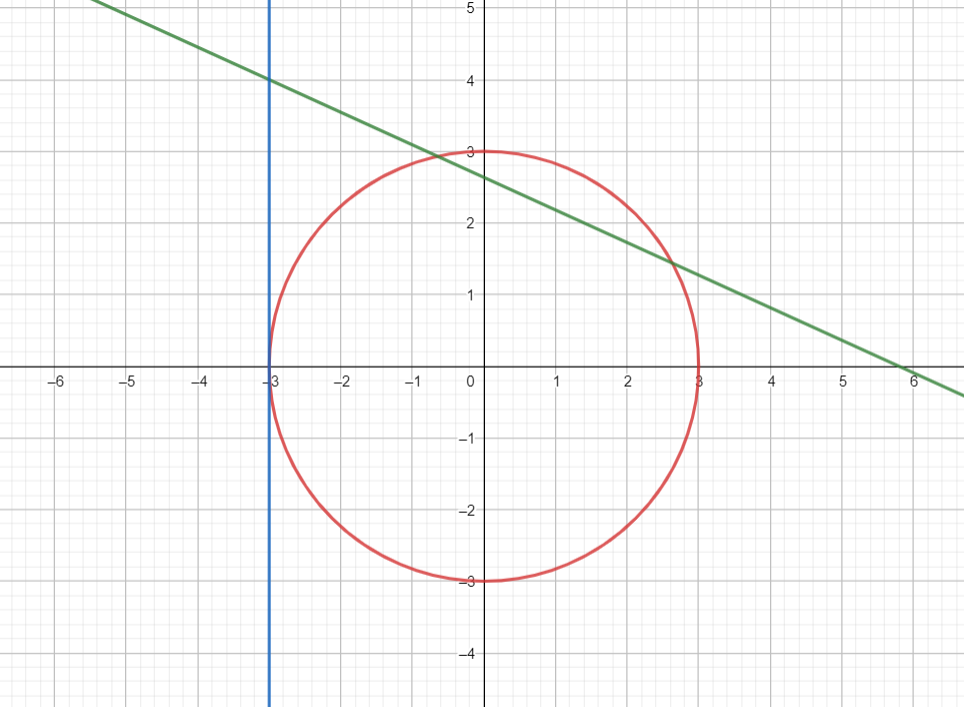
Como o centro da circunferência é a origem, fica fácil ver que o raio nesse caso será 3, logo 3 é um dos valores para k, pois a equação da circunferência está no formato x² + y²= R² (raio R = k).

O outro caso seria quando a circunferência passa pelo ponto de encontro das duas retas:


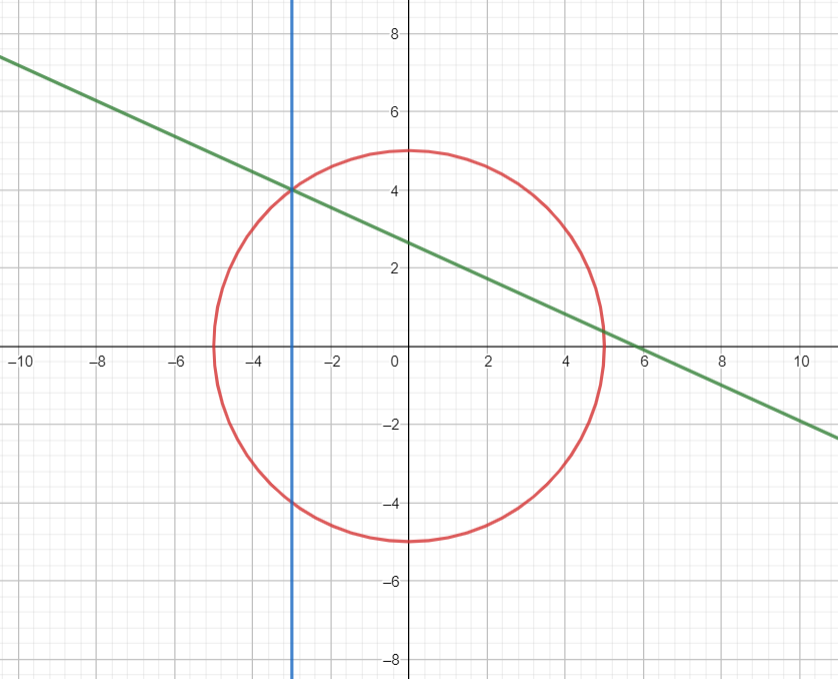
Fazendo a interseção das retas, encontra-se o ponto (-3, 4). Agora basta substitutir esse ponto na equação da circunferência para encontrar o raio R = 5, logo o outro valor para k será 5, e a soma k1 + k2 resulta em 8. Veja que quaisquer outros valores para o raio resultariam em nenhum, 1, 2 ou 4 pontos de tangência.

Software utilizado: GeoGebra