Triângulo, semelhança.

na figura abaixo I é o incentro do triângulo ABC e sabe se que IM//AB e IP//AC calcular a medida do maior lado do triangulo IMP, sendo AB=6 AC=12 BC=9

figura: https://i.servimg.com/u/f19/20/05/25/10/img-2012.jpg
Gab. : 8cm

O desenho está fora de escala: pare que BC > AC e não é verdade.
Sugiro fazer novo desenho

Por I trace as perpendiculares ID em AB, IE em AC e IF em BC ---> ID = IE = IF = r

Maior lado de IMP é IP

A^B C = I^MP ---> A^CB = I^PM = IPF

Fazendo AD = AE = x (tangentes externas) ---> 

BD = 6 - x ---> BF = 6 - x ---> FC = BC - BF ---> FC = 9 - (6 - x) ---> FC = x + 3

EC = FC ---> EC = x + 3

AE + EC = AC ---> x + (x + 3) = 12 ---> x = 9/2

BD = BF = 6 - 9/2 ---> BD = BF = 3/2

EC = FC = 9/2 + 3 ---> EC = FC = 15/2 

Tente completar

vou tentar completar, obrigado!!

Como os triângulos IMP e ABC são semelhantes, o maior lado daquele será paralelo ao maior lado deste.



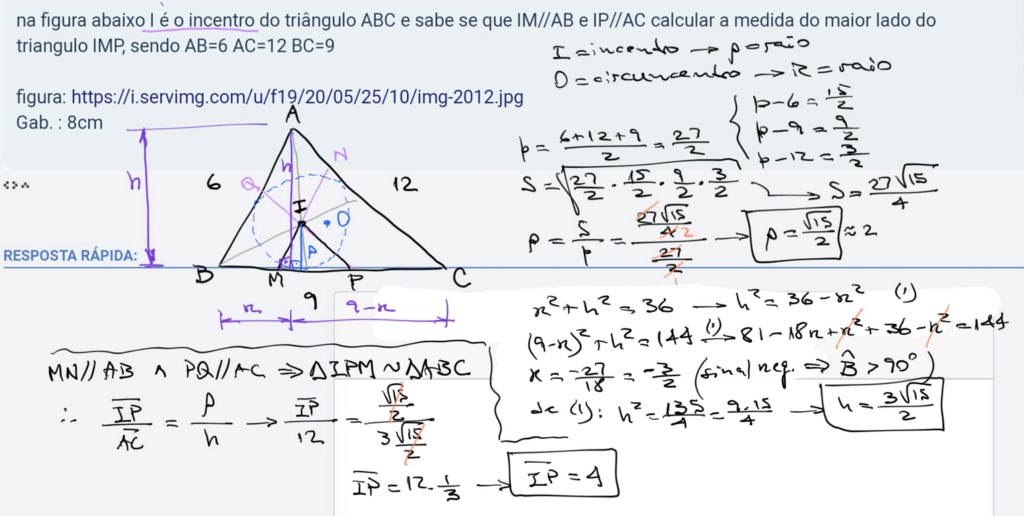
OBS
1) a razão de semelhança foi obtida entre as alturas dos dois triângulos, considerada em relação ao mesmo lado sobre o segmento BC.

2) repetindo a observação já feita na figura: o valor negativo de x (-3/2) deve-se a que, diferente do desenhado, o segmento x fica para o outro lado (do ponto B), ou seja, na realidade o triângulo é obtusângulo com o ângulo ^B > 90°. Isto faz parte de interpretar a solução algébrica. Mas não faz mal, armamos nossas equações com base naquele desenho e devemos continuar usando a lógica delas com esse valor negativo nas equações que montamos para resolver. Evidentemente o x, se desenhado para o lado correto, tem esse mesmo valor em módulo. Se fizermos o desenho com ^B obtuso, teremos outras equações de onde o x sairá positivo. A resposta final será a mesma.

3) bem depois desse trabalho todo percebi que, já tendo a área de ABC, bastava fazer base×altura/2 para obter a altura h. Agora já foi.

ah! não consultei o link. Fiz o desenho conforme achei que era baseado no enunciado.

e a resposta não confere com o gabarito.

Boa noite, tentei resolvê-la por um jeito mais rápido. 
Obs: Gab não bateu, gabarito semelhante ao mestre medeiros

https://i.servimg.com/u/f96/20/57/27/03/captur12.png