Rotação
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Rotação
Rotação
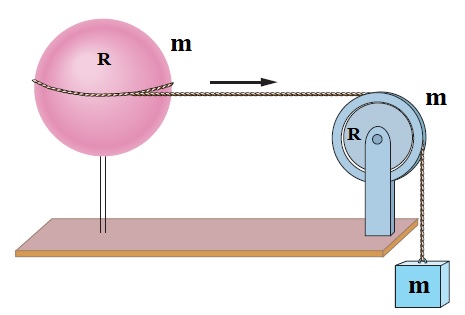
Uma esfera, uma polia e um bloco, todos de massa m = 4,5 kg, conectados por um cabo inextensível de massa desprezível, conforme ilustrado acima, são abandonados a partir do repouso. Sabendo que o raio da esfera e da polia são iguais, de valor R = 20,3 cm, determine a velocidade do bloco após um deslocamento vertical h = 126 cm.
Resposta : 3,61 m/s.

Resposta : 3,61 m/s.

shellbernardes- Iniciante
- Mensagens : 3
Data de inscrição : 25/11/2018
 Re: Rotação
Re: Rotação
Irei considerar que não há atrito e que a corda não desliza em nenhum momento.
Como não há nenhuma força dissipativa podemos considerar conservação de energia.
Perceba que apenas o bloquinho contribui para energia potencial gravitacional.
Por conservação de energia temos que a energia mecânica inicial é igual a final, ou seja:
∆Ec + ∆Ep = 0
∆Ep = -mgh
∆Ec = (Iesfera)(wesfera)²/2 + (Idisco)(wdisco)²/2 + mv²/2 (I)
Considerando que a corda não desliza, essa velocidade v do bloquinho tem que ser igual a velocidade de um ponto da borda do disco e essa mesma velocidade é igual a velocidade de um ponto da borda da esfera, portanto:
v = (wesfera)R = (wdisco)R
Substituindo em (I):
∆Ec = (Iesfera)(wesfera)²/2 + (Idisco)(wdisco)²/2 + mv²/2 (I)
∆Ec = (Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 (I)
Agora vem um problema, o exercício não específica se a esfera é sólida ou se ela é oca,. Para uma esfera sólida temos que seu momento de inércia é dado por (2MR²)/5 e para uma esfera oca, a inércia é dada por (2MR²)/3. Para a polia temos que o momento de inércia é dado por (MR²)/2.
Agora, devido a conservação da energia:
(Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 - mgh = 0
(Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 = mgh
Se a esfera for sólida temos que I = (2MR²)/5.
Substituindo os valores, iremos encontrar v aproximadamente igual a 3,61 m/s.
Se a esfera for oca temos que I = (2MR²)/3.
Substituindo os valores, iremos encontrar v aproximadamente igual a 3,38 m/s.
Aparentemente a esfera do exercício é sólida.
Bem, eu acho que é isso, qualquer coisa é só perguntar.
Como não há nenhuma força dissipativa podemos considerar conservação de energia.
Perceba que apenas o bloquinho contribui para energia potencial gravitacional.
Por conservação de energia temos que a energia mecânica inicial é igual a final, ou seja:
∆Ec + ∆Ep = 0
∆Ep = -mgh
∆Ec = (Iesfera)(wesfera)²/2 + (Idisco)(wdisco)²/2 + mv²/2 (I)
Considerando que a corda não desliza, essa velocidade v do bloquinho tem que ser igual a velocidade de um ponto da borda do disco e essa mesma velocidade é igual a velocidade de um ponto da borda da esfera, portanto:
v = (wesfera)R = (wdisco)R
Substituindo em (I):
∆Ec = (Iesfera)(wesfera)²/2 + (Idisco)(wdisco)²/2 + mv²/2 (I)
∆Ec = (Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 (I)
Agora vem um problema, o exercício não específica se a esfera é sólida ou se ela é oca,. Para uma esfera sólida temos que seu momento de inércia é dado por (2MR²)/5 e para uma esfera oca, a inércia é dada por (2MR²)/3. Para a polia temos que o momento de inércia é dado por (MR²)/2.
Agora, devido a conservação da energia:
(Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 - mgh = 0
(Iesfera)(v)²/(2R²) + (Idisco)(v²)²/(2R²) + mv²/2 = mgh
Se a esfera for sólida temos que I = (2MR²)/5.
Substituindo os valores, iremos encontrar v aproximadamente igual a 3,61 m/s.
Se a esfera for oca temos que I = (2MR²)/3.
Substituindo os valores, iremos encontrar v aproximadamente igual a 3,38 m/s.
Aparentemente a esfera do exercício é sólida.
Bem, eu acho que é isso, qualquer coisa é só perguntar.
fantecele- Fera

- Mensagens : 1225
Data de inscrição : 14/09/2014
Idade : 27
Localização : Nova Venécia-ES, Brasil
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












