Polinômio

por Liliana Rodrigues Sáb 13 Out 2018, 14:25

O valor de k para que a equação 3x³ - (3k + 1)x² + 12x - 5k + 1 = 0 tenha uma das raízes igual a -2 é tal que, o valor da expressão 3^k - \frac{2}{k} é:

a) 79/3
b) 1
c) 8
d) 8/9
e) 19/27

Tentei fazer por x1+ x2+ x3 = -b/a
x1*x2 + x1*x3 + x2*x3 = -d/a
x1*x2*x3= c/a
Com x1= -2
E fui substituindo, mas não deu certo...
Alguém, por gentileza?
Obrigada!!

por **Elcioschin** Sáb 13 Out 2018, 16:43

E porque não postou o passo-a-passo da sua solução? Certamente você errou em contas e não podemos dizer onde:

- 2 + r + s = (3.k + 1)/3 ---> r + s = (3.k + 7)/3 ---> I

r.s - 2.r - 2.s = 12/3 ---> r.s - 2.(r + s) = 4 ---> II

I em II ---> r.s - 2.[ (3.k + 7)/3) = 4 ---> r.s = (6.k + 26)/3 ---> III

-2.r.s = - (- 5.k + 1)/3 ---> r.s = (- 5.k + 1)/6 ---> IV

III = IV ---> (6.k + 26)/3 = (- 5.k + 1)/6 ---> 12.k + 52 = - 5.k + 1 ---> 17.k = - 51 ---> k = - 3

3^k - 2/k = 3-³ - 2/(-3) = 1/27 + 2/3 = 1/27 + 18/27 = 19/27

por Liliana Rodrigues Seg 15 Out 2018, 13:47

3x³ + (-3k - 1)x² + 12x + (-5k +1) = 0

a= 3
b= (-3k - 1)
c= 12
d= (-5k + 1)

x2 + x3= (3k + 7)/3 (i)

x2.x3= (-5k + 1)/3 (ii)

-2.x2 -2.x3 + x2.x3= 4
-2.(x2 + x3) + x2.x3 = 4
-2 (3k + 7)/3 + (-5k +1)/3 = 4
k= -11/25

Onde eu errei?? Neutral

por **Giovana Martins** Seg 15 Out 2018, 15:19

Está dando errado, pois as suas relações de Girard não foram escritas da forma correta.

x1*x2 + x1*x3 + x2*x3 = c/a (forma correta)

x1*x2*x3= -d/a (forma correta)

\\\mathrm{Sendo}\ \alpha =-2:\\\\\alpha +\beta +\gamma =\frac{3k+1}{3}\rightarrow \beta +\gamma =\frac{3k+1}{3}+2\\\\\alpha \beta \gamma =\frac{5k-1}{3}\rightarrow \beta \gamma =\frac{-5k+1}{6}\\\\\alpha \beta +\alpha \gamma +\beta \gamma =\alpha (\beta +\gamma )+\beta \gamma =4\\\\\therefore \ -2\left (\frac{3k+1}{3}+2 \right )+\frac{-5k+1}{6}=4\to k=-3

por **Giovana Martins** Seg 15 Out 2018, 15:21

Além disso:

-2 (3k + 7)/3 + (-5k +1)/3 = 4

No lugar do 3 é 6. Deve ter sido apenas algum erro de continha.

por **Mateus Meireles** Seg 15 Out 2018, 16:48

Olá a todos

Eu não entendi muito bem o motivo de atacar o problema por Girard, mas outro caminho é substituir que -2 é raiz e calcular K direto

3x^3 - (3k + 1)x^2 + 12x -5k +1 = 0

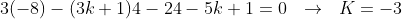
$Polinômio Gif$

Abraço.