Polinômio e fatoração
2 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Polinômio e fatoração
Polinômio e fatoração
Sabe-se que 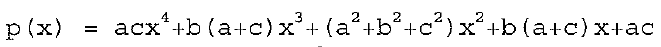 é um produto de dois polinômios do 2° grau e que os números a, b e c são reais não nulos com (b^2 - 4ac) positivo. Nessas condições, é correto afirmar que
é um produto de dois polinômios do 2° grau e que os números a, b e c são reais não nulos com (b^2 - 4ac) positivo. Nessas condições, é correto afirmar que
A)há apenas um valor de x tal que p(x)=0
B)há apenas dois valores de tais que p(x)=0
C)há apenas três valores de x tais que p(x)=0
D)há quatro valores de x tais que p(x)=0
E)não há valores de x tais que p(x)=0
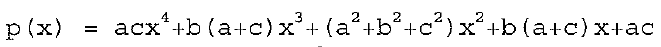 é um produto de dois polinômios do 2° grau e que os números a, b e c são reais não nulos com (b^2 - 4ac) positivo. Nessas condições, é correto afirmar que
é um produto de dois polinômios do 2° grau e que os números a, b e c são reais não nulos com (b^2 - 4ac) positivo. Nessas condições, é correto afirmar queA)há apenas um valor de x tal que p(x)=0
B)há apenas dois valores de tais que p(x)=0
C)há apenas três valores de x tais que p(x)=0
D)há quatro valores de x tais que p(x)=0
E)não há valores de x tais que p(x)=0

Nova Era- Mestre Jedi

- Mensagens : 529
Data de inscrição : 05/11/2017
Idade : 22
Localização : Rio de Janeiro
 Re: Polinômio e fatoração
Re: Polinômio e fatoração
Olá, tudo bem?
Primeiramente devemos reescrever o polinômio de modo a obtermos uma multiplicação entre dois polinômios do segundo grau. Para fazermos isso devemos perceber que o termo de maior grau(acx^4) será a multiplicação entre o termo de maior grau do primeiro polinômio com o segundo, logo temos o seguinte:
p(x) = (ax^2 + kx + y)(cx^2 + zx + w)
Agora, olhando para o termo de menor grau percebemos que yw = ac
Olhando para o termo de grau dois percebemos que w = a e y = c, pois quando multiplicarmos os trinômios teremos a²x^2 e c²x^2
Portanto, obtido esse resultado percebemos que k = z = b, uma vez que, obtidos os resultados anteriores, essa é a única maneira de obtermos bx^2 no resultado final e, consequentemente, o termo de grau dois valendo a^2 + b^2 + c^2
Dessa forma, vamos substituir as incógnitas:
p(x) = (ax^2 + bx + c)(cx^2 + bx + a)
Agora, se igualarmos esse resultado a zero e tirarmos bhaskara dos dois trinômios, encontraremos quatro valores distintos para o x(podendo ser real ou complexo), uma vez que o ∆ = b^2 - 4ac e sabemos, pelo enunciado, que esse resultado é não nulo.
Primeiramente devemos reescrever o polinômio de modo a obtermos uma multiplicação entre dois polinômios do segundo grau. Para fazermos isso devemos perceber que o termo de maior grau(acx^4) será a multiplicação entre o termo de maior grau do primeiro polinômio com o segundo, logo temos o seguinte:
p(x) = (ax^2 + kx + y)(cx^2 + zx + w)
Agora, olhando para o termo de menor grau percebemos que yw = ac
Olhando para o termo de grau dois percebemos que w = a e y = c, pois quando multiplicarmos os trinômios teremos a²x^2 e c²x^2
Portanto, obtido esse resultado percebemos que k = z = b, uma vez que, obtidos os resultados anteriores, essa é a única maneira de obtermos bx^2 no resultado final e, consequentemente, o termo de grau dois valendo a^2 + b^2 + c^2
Dessa forma, vamos substituir as incógnitas:
p(x) = (ax^2 + bx + c)(cx^2 + bx + a)
Agora, se igualarmos esse resultado a zero e tirarmos bhaskara dos dois trinômios, encontraremos quatro valores distintos para o x(podendo ser real ou complexo), uma vez que o ∆ = b^2 - 4ac e sabemos, pelo enunciado, que esse resultado é não nulo.
Última edição por paulinoStarkiller em Qui 16 Ago 2018, 15:06, editado 1 vez(es)

paulinoStarkiller- Fera

- Mensagens : 241
Data de inscrição : 05/08/2018
Idade : 23
Localização : São Paulo - SP
 Re: Polinômio e fatoração
Re: Polinômio e fatoração
Excelentíssima resolução, paulinoStarkiller!
Muito obrigado por me ajudar!!!





Muito obrigado por me ajudar!!!

Nova Era- Mestre Jedi

- Mensagens : 529
Data de inscrição : 05/11/2017
Idade : 22
Localização : Rio de Janeiro
 Tópicos semelhantes
Tópicos semelhantes» Fatoração de polinômio
» Fatoração de Polinômio
» Fatoração de polinômio
» Fatoração de Polinômio
» Fatoração de polinômio
» Fatoração de Polinômio
» Fatoração de polinômio
» Fatoração de Polinômio
» Fatoração de polinômio
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












