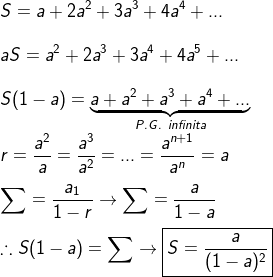Limite da soma
4 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1

Andre Ampère- Recebeu o sabre de luz

- Mensagens : 152
Data de inscrição : 23/12/2017
Idade : 27
Localização : São Luís-MA, Brasil
 Re: Limite da soma
Re: Limite da soma

axell13- Recebeu o sabre de luz

- Mensagens : 164
Data de inscrição : 21/06/2015
Idade : 25
Localização : Santa Luzia, MG, Brazil

Giovana Martins- Grande Mestre

- Mensagens : 8531
Data de inscrição : 15/05/2015
Idade : 24
Localização : São Paulo
 Re: Limite da soma
Re: Limite da soma
Só por curiosidade, também têm outro jeito de resolver, só que é um pouco mais demorado. Enfim....:
Você pode alinhar as variáveis em colunas conforme seu grau, assim a primeira coluna terá um termo, pois só há uma incógnita de grau um. Na segunda coluna terá dois, na terceira, três.....
Primeira coluna: a + a^2+ a^3 + a^4 + .......
Segunda coluna: a^2+ a^3 + a^4 + ......
Terceira coluna: a^3 + a^4 + .......
Quarta coluna: a^4 + .......
Calculando a soma de cada linha através da soma de P.G. infinita:
S1 = a/(1-a)
S2 = (a^2)/(1-a)
S3 = (a^3)/(1-a)
S4 = (a^4)/(1-a)
......
Note que as somas de cada linha também estão em P.G. infinita de razão a.
Calculando a soma das linhas obtemos a resposta:
S = S1 + S2 + S3 + S4 + ....
S = a/(1-a)/(1-a)
Logo:
S = a/(1-a)^2
Você pode alinhar as variáveis em colunas conforme seu grau, assim a primeira coluna terá um termo, pois só há uma incógnita de grau um. Na segunda coluna terá dois, na terceira, três.....
Primeira coluna: a + a^2+ a^3 + a^4 + .......
Segunda coluna: a^2+ a^3 + a^4 + ......
Terceira coluna: a^3 + a^4 + .......
Quarta coluna: a^4 + .......
Calculando a soma de cada linha através da soma de P.G. infinita:
S1 = a/(1-a)
S2 = (a^2)/(1-a)
S3 = (a^3)/(1-a)
S4 = (a^4)/(1-a)
......
Note que as somas de cada linha também estão em P.G. infinita de razão a.
Calculando a soma das linhas obtemos a resposta:
S = S1 + S2 + S3 + S4 + ....
S = a/(1-a)/(1-a)
Logo:
S = a/(1-a)^2

Dylan Chan- Padawan

- Mensagens : 52
Data de inscrição : 31/05/2018
Idade : 22
Localização : São Paulo- São Paulo - Brasil
 Tópicos semelhantes
Tópicos semelhantes» Limite da soma
» Limite da Soma - PG
» [UNESP]Limite da Soma
» Calcule a soma (limite)
» P.G., Limite da Soma "O valor de 1/2 - 1/3.."
» Limite da Soma - PG
» [UNESP]Limite da Soma
» Calcule a soma (limite)
» P.G., Limite da Soma "O valor de 1/2 - 1/3.."
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos