OBF- 3* FASE Nível II-2017(Estática)

Novamente, quem puder disponibilizar a resolução agradeço muito.

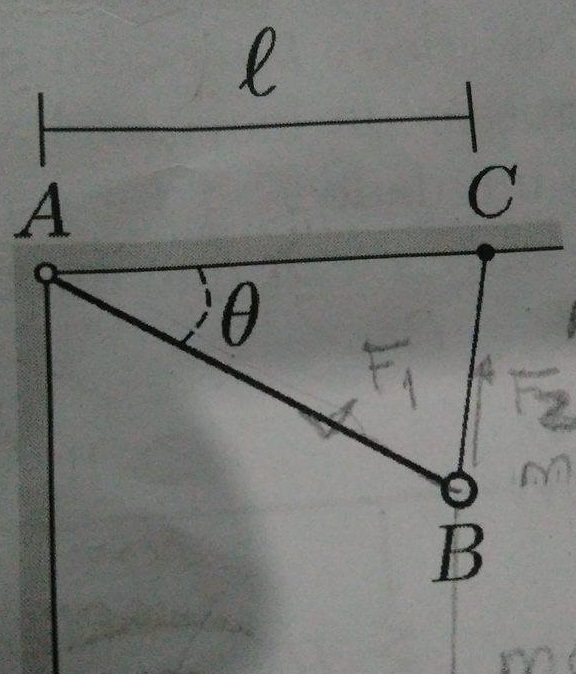
10.A figura abaixo mostra um sistema em equilíbrio estático. A haste homogênea AB de comprimento L=80 cmL=80 cm e massa desprezível está presa à parede vertical por um pino em trono do qual poderia girar livremente. Na extremidade B da haste está presa uma pequena esfera de massa m=200g . Fixada a essa esfera e ao ponto C do teto há um material elástico de constante elástica k=2,50 N/m e que quando relaxado tem comprimento desprezível. Determine (a) o ângulo θ=θo de equilíbrio e (b) o período de oscilação deste sistema se a posição angular θ for levemente deslocada de θo .

AB é igual a AC , pelo que eu entendi.

A )Considerand o ponto B , teremos a força elástica e a força peso agindo , como o sistema para essa condição está em equilíbrio , teremos a seguinte igualdade de forças , perceba a geometria do problema , qualquer coisa eu posto uma foto com o diagrama e ângulos.

m.g.cos(theta)=Fel.cos(theta/2)
2.cos(theta)=2,5.x.cos(theta/2)

Repare que no enunciado ele diz que o comprimento do elástico sem deformação é desprezível , ou seja , x é igual a CB (segmento).

Pela lei dos cossenos no triângulo ABC , temos que.:

x=2.0,8.sen(theta/2)

Substituindo na fórmula da igualdade das forças , temos :

2.cos(theta)=2,5.2.0,8.sen(theta/2).cós(theta/2)
2.cos(theta)=2.sen(theta)
TG(theta)=1.

Theta=45°

B) Agora deslocando de um ângulo (theta 0) , temos que a força restauradora é dada por .:

F resta= 2,5.x'.cos[(theta+theta0)/2] - 2.cos[(theta+theta0)/2]

Pela lei dos cossenos e determinando x' , teremos .:

F resta= 2( sen(theta+theta0)- cós(theta+theta0))

Colocando em evidência V2 , para aparecer o seno e o cosseno de 45° , temos.:

F rest=2(sem(theta+theta0-45°))

Mas theta =45°
Logo

F rest=V2.2.sen(theta0)

Como theta 0 é bem pequeno podemos usar sem(theta0)=dx/0,8 , sendo 'dx' o quanto a corda foi puxada para baixo.

Logo F rest=2.V2.dx/0,8

Só substituir na equação do período .