Tetraedro regular
+2
AlessandroMDO
Liliana Rodrigues
6 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
Tetraedro regular
por Liliana Rodrigues Dom 09 Jul 2017, 19:52
(Fuvest) Em um tetraedro regular de lado a, a distância entre os pontos médios de duas arestas não adjacentes é igual a:
a) a √3
b) a √2
c) a √3/2
d) a √2/2
e) a√2/4
a) a √3
b) a √2
c) a √3/2
d) a √2/2
e) a√2/4
Liliana Rodrigues- Estrela Dourada
- Mensagens : 2082
Data de inscrição : 16/03/2016
Idade : 27
Localização : Ribeirão Preto - SP
Re: Tetraedro regular
por AlessandroMDO Dom 09 Jul 2017, 20:33
Como ele está colocado bem sobre o ponto médio das arestas, os triângulos verdes que ele forma são todos equiláteros de aresta a/2.
Ou seja, os dois lados azuis valem a/2 também. Por Pitágoras:
x²= (a/2)²+(a/2)²
x²= a²/4 + a²/4
x²= 2a²/4
x = a√2/2
- Spoiler:
Ou seja, os dois lados azuis valem a/2 também. Por Pitágoras:
x²= (a/2)²+(a/2)²
x²= a²/4 + a²/4
x²= 2a²/4
x = a√2/2
AlessandroMDO- Jedi
- Mensagens : 436
Data de inscrição : 20/09/2016
Idade : 24
Localização : Ipuã - SP
Re: Tetraedro regular
por Liliana Rodrigues Dom 09 Jul 2017, 21:03
Eu não consegui entender como forma triângulo equilátero em cima. Se cada face é um triângulo equilátero, então seus ângulos são todos 60º. Então ali do lado, 60+60= 120º, e pela leis dos cossenos, eu achei que o lado referente ao ângulo de 120º= a√3/4. Usando geometria e achando os ângulos, eu encontrei que o triângulo verde em baixo realmente é equilátero, aí fazendo por Pitágoras dá x=a. Não entendi por que ali em cima é equilátero...
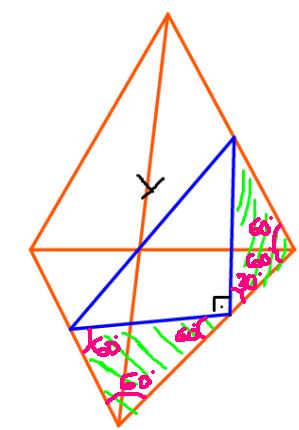
Liliana Rodrigues- Estrela Dourada
- Mensagens : 2082
Data de inscrição : 16/03/2016
Idade : 27
Localização : Ribeirão Preto - SP
Re: Tetraedro regular
por AlessandroMDO Dom 09 Jul 2017, 21:48
Calculando a altura desse triângulo usando o triângulo da direita:
(a/2)² = h² +(a/4)²
a²/4 = h² +a²/16
a²/4 - a²/16 = h²
3a²/16 = h²
h = a√3/4
Sabendo a altura, pode-se calcular a aresta azul do triângulo da esquerda:
x² = (a/4)²+(a√3/4)²
x² = a²/16+(a².3/16)
x²= 4a²/16
x²= a²/4
x = a/2, que é a medida do traçado azul. Ou seja, ele é equilátero.
Em relação aos ângulos, você está confundindo os planos, você está considerando o lado de baixo e o lado de trás, enquanto estamos analisando somente o lado da frente:
Na figura não fica claro, pois está toda fora de forma mas o segmento azul é paralelo à aresta da esquerda, sendo cortado pela reta em baixo, ou seja, o ângulo de 60º do canto esquerdo é o mesmo ângulo do canto direito encostado na reta azul. O mesmo vale para o ângulo superior.
- Spoiler:
(a/2)² = h² +(a/4)²
a²/4 = h² +a²/16
a²/4 - a²/16 = h²
3a²/16 = h²
h = a√3/4
Sabendo a altura, pode-se calcular a aresta azul do triângulo da esquerda:
x² = (a/4)²+(a√3/4)²
x² = a²/16+(a².3/16)
x²= 4a²/16
x²= a²/4
x = a/2, que é a medida do traçado azul. Ou seja, ele é equilátero.
Em relação aos ângulos, você está confundindo os planos, você está considerando o lado de baixo e o lado de trás, enquanto estamos analisando somente o lado da frente:
- Spoiler:
Na figura não fica claro, pois está toda fora de forma mas o segmento azul é paralelo à aresta da esquerda, sendo cortado pela reta em baixo, ou seja, o ângulo de 60º do canto esquerdo é o mesmo ângulo do canto direito encostado na reta azul. O mesmo vale para o ângulo superior.
Última edição por AlessandroMDO em Seg 10 Jul 2017, 10:39, editado 1 vez(es)
AlessandroMDO- Jedi
- Mensagens : 436
Data de inscrição : 20/09/2016
Idade : 24
Localização : Ipuã - SP
Re: Tetraedro regular
por Medeiros Dom 09 Jul 2017, 23:09
O Alessandro obteve a resposta do gabarito mas não vi sentido nos desenhos dele, então nem acompanhei a sua resolução.
De qualquer forma, essa questão já foi resolvida no fórum pelo menos duas vezes. Veja:
https://pir2.forumeiros.com/t78283-tetraedro
e
https://pir2.forumeiros.com/t105448-distancia-entre-arestas-de-uma-piramide
De qualquer forma, essa questão já foi resolvida no fórum pelo menos duas vezes. Veja:
https://pir2.forumeiros.com/t78283-tetraedro
e
https://pir2.forumeiros.com/t105448-distancia-entre-arestas-de-uma-piramide
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Tetraedro regular
por AlessandroMDO Seg 10 Jul 2017, 00:15
De fato, os desenhos ficaram um lixo 
- Spoiler:
AlessandroMDO- Jedi
- Mensagens : 436
Data de inscrição : 20/09/2016
Idade : 24
Localização : Ipuã - SP
Re: Tetraedro regular
por Medeiros Seg 10 Jul 2017, 01:50
Perfeito, Alessandro, entendi agora.
Você tomou as bases médias dos triângulos equiláteros das faces e calculou a hipotenusa de um triângulo retângulo isósceles.
Ficou uma solução simples e fácil/rápida. Mas você partiu do fato de que aquele ângulo é reto sem antes tê-lo demonstrado. Como você sabia que o ângulo é reto?
Você tomou as bases médias dos triângulos equiláteros das faces e calculou a hipotenusa de um triângulo retângulo isósceles.
Ficou uma solução simples e fácil/rápida. Mas você partiu do fato de que aquele ângulo é reto sem antes tê-lo demonstrado. Como você sabia que o ângulo é reto?
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Tetraedro regular
por AlessandroMDO Seg 10 Jul 2017, 02:22
De fato, apenas o considerei. Pareceu tão óbvio que sequer pensei na possibilidade de não ser reto. Você conhece alguma maneira de demonstrar?
AlessandroMDO- Jedi
- Mensagens : 436
Data de inscrição : 20/09/2016
Idade : 24
Localização : Ipuã - SP
Re: Tetraedro regular
por Medeiros Seg 10 Jul 2017, 02:38
Indiretamente você acaba de mostrar.
Se considerarmos a distância d calculada pelos links acima, pode-se aplicar a lei dos cossenos no seu triângulo vermelho e obter o valor do ângulo.
Se considerarmos a distância d calculada pelos links acima, pode-se aplicar a lei dos cossenos no seu triângulo vermelho e obter o valor do ângulo.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Tetraedro regular
por gabriel.ricci.oliveira.95 Ter 15 Out 2019, 22:09
Alguem poderia me explicar porque o triangulo formado é retangulo?
gabriel.ricci.oliveira.95- Recebeu o sabre de luz
- Mensagens : 134
Data de inscrição : 30/09/2019
Idade : 29
Localização : sao jose dos campos
Página 1 de 2 • 1, 2
Tópicos semelhantesPágina 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
