Ponto que não existe
2 participantes
Página 1 de 1
 Ponto que não existe
Ponto que não existe
Galera, Tudo bom com vcs?
Então, a dúvida de hoje é sobre o que acontece com valores de x que não existem na derivada(2° ou 1°), mas que existem na função principal?
Exemplo
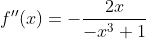
Eu estou ciente que f''(x)=0 se x for igual a 0, mas e f''(1)?? Não existe, eu sei. Qual a consequência para o gráfico??
Só pra deixar completinho, a primeira derivada é:
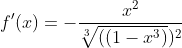
Então, a dúvida de hoje é sobre o que acontece com valores de x que não existem na derivada(2° ou 1°), mas que existem na função principal?
Exemplo
Eu estou ciente que f''(x)=0 se x for igual a 0, mas e f''(1)?? Não existe, eu sei. Qual a consequência para o gráfico??
Só pra deixar completinho, a primeira derivada é:
nadadeiro- Recebeu o sabre de luz

- Mensagens : 191
Data de inscrição : 08/03/2016
Idade : 28
Localização : Rio de Janeiro
 Re: Ponto que não existe
Re: Ponto que não existe
certeza que essa derivada segunda está certa?
![f'(x)=-\frac{x^2}{(1-x^3)^\frac{2}{3}}\\f''(x)=-\frac{ [2x(1-x^3)^\frac{2}{3})-x^2.\frac{2}{3}(1-x^3)^\frac{-1}{3}.(-3x^2)]}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x(1-x^3)^\frac{2}{3}-\frac{2x^4}{(1-x^3)^\frac{1}{3}}}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x[(1-x^3)^\frac{2}{3}+\frac{x^3}{(1-x^3)^\frac{1}{3}}]}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x[1-x^3+x^3]}{(1-x^3)^\frac{5}{3}}=\frac{-2x}{(1-x^3)^\frac{5}{3}}](https://latex.codecogs.com/gif.latex?f'(x)=-\frac{x^2}{(1-x^3)^\frac{2}{3}}\\f''(x)=-\frac{&space;[2x(1-x^3)^\frac{2}{3})-x^2.\frac{2}{3}(1-x^3)^\frac{-1}{3}.(-3x^2)]}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x(1-x^3)^\frac{2}{3}-\frac{2x^4}{(1-x^3)^\frac{1}{3}}}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x[(1-x^3)^\frac{2}{3}+\frac{x^3}{(1-x^3)^\frac{1}{3}}]}{(1-x^3)^\frac{4}{3}}\\f''(x)=\frac{-2x[1-x^3+x^3]}{(1-x^3)^\frac{5}{3}}=\frac{-2x}{(1-x^3)^\frac{5}{3}})
1 não existe em nenhuma das funções. No caso em questão, em 1 teríamos uma assíntota vertical x=1.
=-\infty)
Dando um exemplo que acontece o que vc mencionou:
f(x)=x^{2/3}
f'(x)=2/3 . x^{-1/3}
f'(x) não existe para x=0
então em x=0 f(x) ''bico'': se f'(x) não existe em 0, então em x=0 f'(x)=tg(theta)
se f'(x) não existe tg theta n existe, theta =90.
se em ambos lados, 0 pela direita e pela esquerda não existem, significa que em ambos lados o gráfico é vertical inicialmente,
para essa função, sabemos pela derivada, que á medida que aumentamos x para maior que 0, a derivada é positiva e tende a 0.
à medida que diminuimos x ( para valores negativos) a derivada é negativa e tbm tende a 0 justificando essa forma de bico.
1 não existe em nenhuma das funções. No caso em questão, em 1 teríamos uma assíntota vertical x=1.
Dando um exemplo que acontece o que vc mencionou:
f(x)=x^{2/3}
f'(x)=2/3 . x^{-1/3}
f'(x) não existe para x=0
então em x=0 f(x) ''bico'': se f'(x) não existe em 0, então em x=0 f'(x)=tg(theta)
se f'(x) não existe tg theta n existe, theta =90.
se em ambos lados, 0 pela direita e pela esquerda não existem, significa que em ambos lados o gráfico é vertical inicialmente,
para essa função, sabemos pela derivada, que á medida que aumentamos x para maior que 0, a derivada é positiva e tende a 0.
à medida que diminuimos x ( para valores negativos) a derivada é negativa e tbm tende a 0 justificando essa forma de bico.
LPavaNNN- Grupo
Velhos amigos do Fórum
- Mensagens : 933
Data de inscrição : 22/04/2012
Idade : 30
Localização : Goiânia/GO Brasil
 Re: Ponto que não existe
Re: Ponto que não existe
Realmente lucas. Não saiu a raiz na segunda derivada no latex não sei porque, mas é foi a que você achou. Obrigado, deu pra entender o que o raciocínio!
nadadeiro- Recebeu o sabre de luz

- Mensagens : 191
Data de inscrição : 08/03/2016
Idade : 28
Localização : Rio de Janeiro
 Tópicos semelhantes
Tópicos semelhantes» Existe Limite?
» O limite existe?
» CH₃⁺ existe?
» Por que não existe o ion NO4 -3 ?
» Prove que não existe
» O limite existe?
» CH₃⁺ existe?
» Por que não existe o ion NO4 -3 ?
» Prove que não existe
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












