Sistema cartesiano e ponto

por GabriellaGarcia 17/4/2017, 9:47 pm

Olá!
Alguém poderia me ajudar com essa questão? Eu tentei fazer com a fórmula do baricentro, porém, não cheguei ao resultado correto!
(UECE) Se o ponto P1(x1, y1) é equidistante dos pontos
O(0, 0), M(7, –7) e N(8, 0), então x1²+y1² é igual a:
A) 13
B) 17
C) 25
D) 29
E) n.d.a.

Resp: C

por **Elcioschin** 17/4/2017, 10:36 pm

Calcule o ponto médio P de ON e determine a equação da mediatriz de ON

Calcule o ponto médio Q de MN e determine o coeficiente angular da reta MN

Calcule a equação da mediatriz de MN (passa por P e é perpendicular à reta MN)

O ponto equidistante de O, M, N é o encontro das duas mediatrizes (centro do círculo circunscrito ao triângulo OMN)

por GabriellaGarcia 18/4/2017, 12:51 am

Elcioschin, obrigada pela ajuda! Poderia verificar se está correto dessa forma?

Dop²=Dmp²=Dnp²

Dop²=Dmp²⇒ (x1-0)²+(y1-0)²= (x1-7)²+(y1+7)²⇒
⇒ x1²+y1²= x1²-14x1+49+y1²+14y1+49⇒

⇒ 14x1-14y1-98=0⇒ 2x1-2y1-14=0 (I)

Dop²=Dnp²
(x1-0)²+(y1-0)²= (x1-8 )²+(y1-0)²⇒
⇒x1²+y1²= x1²-16x1+64+y1²⇒

⇒16x1=64⇒ 16x1/8=64/8⇒ 2x1=8 ⇔ x1=4 (II)

(II) em (I):
2.4-2y1-14=0 ⇒ 8-14=2y1⇒ -6=2y1 ⇔ y1= -3

x1²+y1²= 4²+ (-3)²⇒ x1²+y1²= 16+9 ⇔ x1²+y1²= 25

por **Medeiros** 18/4/2017, 3:11 am

Sem fazer muita conta, apenas um esboço das coordenadas.
Apesar de que a graça da questão é mesmo resolver por analítica para treinar.
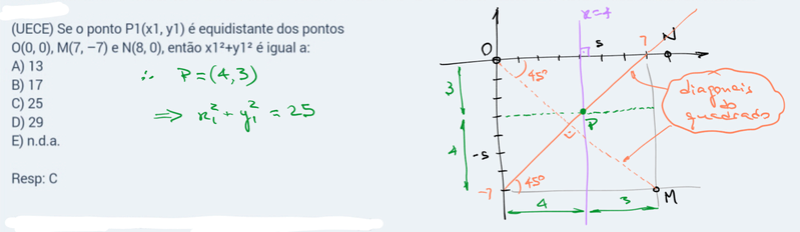
Sistema cartesiano e ponto 2017-136

por Bruno1681 23/9/2021, 12:38 pm

Elcioschin escreveu:Calcule o ponto médio P de ON e determine a equação da mediatriz de ON

Calcule o ponto médio Q de MN e determine o coeficiente angular da reta MN

Calcule a equação da mediatriz de MN (passa por P e é perpendicular à reta MN)

O ponto equidistante de O, M, N é o encontro das duas mediatrizes (centro do círculo circunscrito ao triângulo OMN)

Não consigo visualizar essa resolução e entender o que você quer dizer com a equação da mediatriz ( é uma equação da reta?)

Provavelmente me falta alguns conceitos, mas se possível alguém consegue me explicar de forma menos direta.

por **Elcioschin** 24/9/2021, 12:32 pm

A mediatriz de um segmento de reta AB é uma reta r perpendicular ao segmento e que passa pelo seu ponto médio M.
Note que qualquer ponto da mediatriz é equidistante de A e de B

Como um triângulo tem 3 lados (3 segmentos de reta) ele tem três mediatrizes.

O ponto de encontro de duas (ou das três mediatrizes) é o centro C da circunferência circunscrita ao triângulo: a distância de C aos três vértices é o raio da circunferência.