retas paralelas

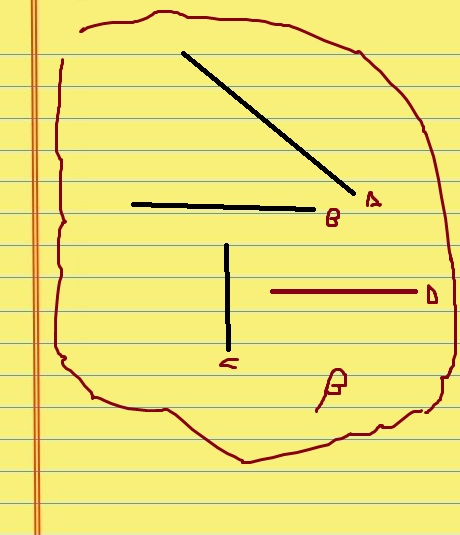
eu desenhei um plano Beta ai coloquei retas A,B,C,D eu queria saber se elas são paralelas distintas

retas paralelas distintas são duas retas de um mesmo plano e não tem pontos em comum ou seja não se cruzam . e na figura nenhuma tem ponto em comum e estão no mesmo plano , elas são paralelas ????   ou para ser paralelas elas tem que ficar igual a linha do caderno  ???


retas concorrentes e paralelas distintas e coincidentes obrigatoriamente tem que ser coplanares?

Vamos ver exatamente o que você fez e depois vamos nos recolher à diminuta insignificância da nossa dimensão humana (ou de macacos pelados, prefiro esta última acepção).

Você delimitou uma região da folha do caderno e chamou isso de plano beta. E isso é tudo o que conseguimos fazer, ou seja, uma representação. Na realidade O PLANO É INFINITO, extravasa a folha do caderno, o tampo da mesa, atravessa as galáxias e vai além (aonde nem a Enterprise vai! he he).

Também as retas são infinitas -- percorrem toda a extensão do plano. Tudo o que desenhamos é um segmento para representá-las.

Portanto o que você desenhou foram segmentos, prolongue-os até o fim da vida e se nunca eles se encontrarem podemos começar a desconfiar que são paralelos. A boa notícia é que podemos, também, usar os conceitos da geometria para obter a mesma conclusão em menos tempo (do que a nossa vida inteira).

Releve minha brincadeira, faço assim porque guardamos melhor uma informação que nos provoca alguma emoção.