Representação gráfica

Dada a função vetorial v=i+(4cost+8sint-1)j+(4cost-8sint)k, descreva o movimento da ponta do vetor v.
A resposta é que o movimento se dá em uma elipse, e consegui esboçá-la escolhendo valores convenientes de t, como 0, pi/2, pi e 3pi/2. Mas como eu posso obter a equação da elipse, para que assim eu a desenhe sem ter que escolher valores para t?

Boa noite. 

Temos aqui um vetor da forma  no espaço . A meu ver, o movimento da ponta deste vetor ocorrerá no plano 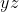, pois  não depende do parâmetro t, como pode ser visto na forma apresentada no enunciado:

.


Para entender como ocorre esse movimento, uma saída é "eliminarmos" o parâmetro t, obtendo assim uma relação entre as coordenadas y e z de um ponto  do plano yz. Apenas para facilitar minha vida, farei algumas alterações... 

4cost = a
8sent = b

 ... (I)
 ... (II)

(I)+(II)

 ... (III)

Isolando a e substituindo em II (ou I, tanto faz):

 ... (IV)

(III)²+(IV)²





Essa é a equação de uma elipse inclinada no plano yz. Para rotacioná-la, precisamos encontrar um ângulo conveniente para isso. Nesse caso, utilizarei a matriz de rotação no sentido anti-horário (veja http://obaricentrodamente.blogspot.com.br/2011/06/matrizes-de-rotacao-no-r2.html).









Olhando para a equação da elipse inclinada, parece conveniente escolher um valor de  que elimine termos contendo o produto , que caracterizam a rotação da cônica. Nesse caso, rotacionamos a elipse de um ângulo , pois . Então:




Substituindo o resultado obtido na equação da elipse, ficamos com





que é a mesma elipse, só que inclinada de 45° no sentido anti-horário. Assim fica mais fácil tentar esboçá-la em um gráfico. Desenhe a cônica no plano y'z' e depois desenhe o plano yz(eixos y e z) com o eixo y fazendo um ângulo de 45° com o eixo y'. Experimente este site: https://www.desmos.com/calculator.

Acredito ser isso.