PUC( 2015
3 participantes
Página 1 de 1
PUC( 2015
por gabrieldavid Dom 27 Nov 2016, 10:39
Uma urna tem 9 bolas, cada uma marcada com uma das letras de A a I:
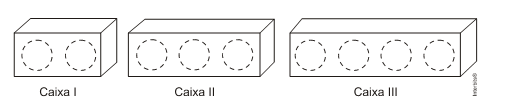
Esmeralda sorteia duas bolas para entrarem na caixa I, três bolas para entrarem na caixa II, e as quatro bolas restantes são colocadas na caixa III.
a) Qual é a probabilidade de que a bola A esteja na caixa I? GAB = 2/9
b) Qual é a probabilidade de que haja exatamente uma bola com vogal na caixa I?GAB= 1/2
c) Qual é a probabilidade de que haja uma bola com vogal em cada caixa? GAB = 2/7
Esmeralda sorteia duas bolas para entrarem na caixa I, três bolas para entrarem na caixa II, e as quatro bolas restantes são colocadas na caixa III.
a) Qual é a probabilidade de que a bola A esteja na caixa I? GAB = 2/9
b) Qual é a probabilidade de que haja exatamente uma bola com vogal na caixa I?GAB= 1/2
c) Qual é a probabilidade de que haja uma bola com vogal em cada caixa? GAB = 2/7
gabrieldavid- Recebeu o sabre de luz
- Mensagens : 166
Data de inscrição : 15/03/2014
Idade : 31
Localização : Rio de Janeiro
Re: PUC( 2015
por EstudandoProITA Dom 27 Nov 2016, 11:42
a) Considere o espaço amostral: (9 2).(7 3).
Quantas formas posso arrumar em combinação para que A esteja em 1? 8 . (7 3).
Logo a resposta é 8 / (9 2) = 2/9.
b) Mesmo espaço amostral, mas o evento muda.
Temos 3 vogais, então:
3.1.(6 1).(7 3)/ [(9 2).(7 3)] = 1/2.
c)Agora temos que ter uma bola com vogal em cada caixa:
[1.(6 1)].[1.(5 2).6]/[(9 2).(7 3)]= 2/7.
*Repare que não utilizei e nenhum caso a contagem na terceira caixa, pois as que estão lá, são os restos.
*Na letra b eu multiplico por 3, pois há 3 vogais.
*Multipliquei por 6 na questão c para que tenha a possibilidade de as caixas trocarem as vogais.
Bis gleich.
Quantas formas posso arrumar em combinação para que A esteja em 1? 8 . (7 3).
Logo a resposta é 8 / (9 2) = 2/9.
b) Mesmo espaço amostral, mas o evento muda.
Temos 3 vogais, então:
3.1.(6 1).(7 3)/ [(9 2).(7 3)] = 1/2.
c)Agora temos que ter uma bola com vogal em cada caixa:
[1.(6 1)].[1.(5 2).6]/[(9 2).(7 3)]= 2/7.
*Repare que não utilizei e nenhum caso a contagem na terceira caixa, pois as que estão lá, são os restos.
*Na letra b eu multiplico por 3, pois há 3 vogais.
*Multipliquei por 6 na questão c para que tenha a possibilidade de as caixas trocarem as vogais.
Bis gleich.
EstudandoProITA- Padawan
- Mensagens : 71
Data de inscrição : 15/11/2016
Idade : 25
Localização : Curitiba
Re: PUC( 2015
por ALEXZOE Dom 27 Nov 2016, 15:53
Outra resolucao um pouco diferente:
a) Temos duas opcoes para a bola A esta na caixa I de um total de 9 opcoes. Logo, P=2/9. Ou:
resultados favoraveis:
C 1,1 * C 8,1 = 1*8 = 8
resultados possiveis:
C 9,2=36
Probabilidade desejada:
P = 8/36 = 2/9.
b) Vogal na caixa I.
resultados favoraveis:
C 3,1 * C 6,1 = 3*6 = 18 maneiras.
Total de casos possiveis:
C 9,2 = 36 maneiras.
logo, P = 18/36 = 1/2.
c) Resultados favoraveis:
(3 * C 6, 1) * (2 * C 5,3) * C 4,4 = 360
Resultados possiveis:
C 9,2 *C 7,3 * C 4, 4 = 1260.
Probabilidade desejada:
P = 360/1260 = 2/7
a) Temos duas opcoes para a bola A esta na caixa I de um total de 9 opcoes. Logo, P=2/9. Ou:
resultados favoraveis:
C 1,1 * C 8,1 = 1*8 = 8
resultados possiveis:
C 9,2=36
Probabilidade desejada:
P = 8/36 = 2/9.
b) Vogal na caixa I.
resultados favoraveis:
C 3,1 * C 6,1 = 3*6 = 18 maneiras.
Total de casos possiveis:
C 9,2 = 36 maneiras.
logo, P = 18/36 = 1/2.
c) Resultados favoraveis:
(3 * C 6, 1) * (2 * C 5,3) * C 4,4 = 360
Resultados possiveis:
C 9,2 *C 7,3 * C 4, 4 = 1260.
Probabilidade desejada:
P = 360/1260 = 2/7
ALEXZOE- Recebeu o sabre de luz
- Mensagens : 145
Data de inscrição : 23/09/2016
Idade : 36
Localização : MAMANGUAPE, PB, BRASIL
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
