Geometria Cefet

por dragon2306 Seg 20 Jun 2016, 22:24

Três triangulos equiláteros de lado 1cm estão enfileirados como indicado na figura abaixo. Nessa condição, determine o seno do angulo θ

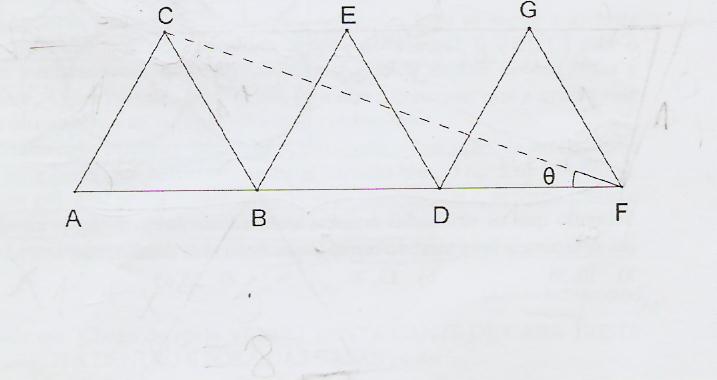
Geometria Cefet 003

Alguem pode resolver sem usar lei dos senos .

por gabriel e. Seg 20 Jun 2016, 22:41

Boa noite,

Trace uma reta do ponto C até até o ponto médio de AB, formando assim um ângulo de 90º. Vamos chamar esse ponto de M
O triângulo CMF é retângulo com catetos medindo CM e MF
CM=√3/2 (pois é a altura do triângulo)
MF= 1+1+1/2=5/2
Por pitagoras:
(FC)^2=(CM)^2+(MF)^2=3/4+25/4=28/4
FC=√28/2=√7

O seno do ângulo será o cateto oposto a ele (CM) dividido pela hipotenusa (CF) que é igual a (√3/2)/√7=√21/14

por **Ashitaka** Seg 20 Jun 2016, 22:47

Outro modo (mais algébrico):
sendo h a altura do triângulo ACB e a o lado:
h = asen60 ----> h/a = sen60°

tgθ = h/(2a + a/2) = 2h/(5a) = 2sen60°/5 = √3/5
tg²θ + 1 = 28/25
cos²θ = 25/28
sen²θ = 1 - cos²θ = 3/28
senθ = √3/(2√7) = √(21)/14