Área máxima de um retângulo com perímetro p

por jvdbosa Qui 16 Jun 2016, 18:24

Dado um retângulo de perímetro p, prove que a maior área possível é um quadrado, ou seja, quando os lados x e y são iguais.

Resposta:

Perimetro:
$p = 2x+2y$

O perímetro é constante então podemos reescrever:
$x=p/2-y$

Área:
$A=xy$
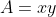
Substituindo x:
$A=(p/2-y)*y$
$A=py/2-y^2$
O macete agora é completar o quadrado:
$A=p^2/16-(y-p/4)^2$

Agora fica fácil ver que a área é máxima quando a parte negativa é zero, ou seja, $y-p/4=0$

Isso quer dizer que a área é máxima quando um dos lados do retângulo é igual a 1/4 do perímetro! $y=p/4$

Como um retângulo só tem 4 lados, é fácil ver quer x precisa ser igual y.
$p = 2x+2y=2x+2(p/4)$
$\therefore x=p/4$

Além disso também concluímos que a área máxima de um retângulo (área de um quadrado) é $p^2/16$

por rihan Qui 28 Jul 2016, 21:05

Talvez seja mais um motivo de se usar a noção de semiperímetro:

Sejam:

Perímetro := 2p

Semiperímetro := p

2p = 2x + 2y

p = x + y

y = p - x

A(x,y) = xy

A(x) = x(p - x)

A(x) = px - x²

A(x) é Trinômio 2º grau com:

a = -1 < 0 --> Concavidade para baixo ( ∩ tristinha ) --> Vértice é Máximo
b = p
c = 0

x do Vértice : -b/2a = p/2

y = p - x = p - p/2 = p/2 = x

Se x = y Retângulo é Quadrado

Área Máxima = x.y = x.x = x²= p²/4 ■

Área máxima de um retângulo com perímetro p

Área máxima de um retângulo com perímetro p

Re: Área máxima de um retângulo com perímetro p

Um fórum livre e democrático.