IME - 1990
2 participantes
Página 1 de 1
 IME - 1990
IME - 1990
Considere a família de retas representadas pela equação: 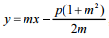 , onde p é uma constante positiva dada e m um número real variável.
, onde p é uma constante positiva dada e m um número real variável.
a)Determine a condição para que num ponto M = (x0, y0) do plano cartesiano, passem duas retas dessa família.
b)Determine o LG dos pontos M para os quais as retas que por eles passem sejam perpendiculares.
Resposta: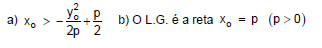
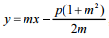 , onde p é uma constante positiva dada e m um número real variável.
, onde p é uma constante positiva dada e m um número real variável. a)Determine a condição para que num ponto M = (x0, y0) do plano cartesiano, passem duas retas dessa família.
b)Determine o LG dos pontos M para os quais as retas que por eles passem sejam perpendiculares.
Resposta:
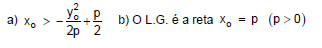
jaques104- Recebeu o sabre de luz

- Mensagens : 149
Data de inscrição : 06/10/2012
Idade : 26
Localização : salvador, BA, Brasil
 Re: IME - 1990
Re: IME - 1990
Se passam em (x0, y0) para duas retas distintas, então teremos que para m diferentes. Primeiro isolamos m:
y = mx - p(1+m²)/(2m)
2my = 2m²x - p - pm²
m²(2x-p) - 2m(y) - p = 0
∆ = 4[ y² + p * (2x-p) ] = 4[ y² +2xp - p² ]
Para que passem duas retas diferentes, é necessário que m seja diferente. Ou seja, o valor do discriminante(∆) deve ser maior que zero, logo:
y²+2xp-p² > 0
y² > p² - 2xp
Ou, se isolarmos x:
2xp > p²-y²
x > (p/2) - (y²/2p)
Para que duas retas sejam perpendiculares, é necessário que o produto dos coeficientes seja equivalente a -1:
m₁*m₂ = -1
Mas como m₁ e m₂ são raizes do polinômio m²(2x-p) - 2m(y) - p, então por Girard temos:
-p/(2x-p) = -1 ---> p = 2x - p ---> x = p
y = mx - p(1+m²)/(2m)
2my = 2m²x - p - pm²
m²(2x-p) - 2m(y) - p = 0
∆ = 4[ y² + p * (2x-p) ] = 4[ y² +2xp - p² ]
Para que passem duas retas diferentes, é necessário que m seja diferente. Ou seja, o valor do discriminante(∆) deve ser maior que zero, logo:
y²+2xp-p² > 0
y² > p² - 2xp
Ou, se isolarmos x:
2xp > p²-y²
x > (p/2) - (y²/2p)
Para que duas retas sejam perpendiculares, é necessário que o produto dos coeficientes seja equivalente a -1:
m₁*m₂ = -1
Mas como m₁ e m₂ são raizes do polinômio m²(2x-p) - 2m(y) - p, então por Girard temos:
-p/(2x-p) = -1 ---> p = 2x - p ---> x = p
____________________________________________
← → ↛  ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥
 ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
 ℛ ℜ ℰ ℳ ℊ ℒ
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Re: IME - 1990
Re: IME - 1990
Muito Obrigado
jaques104- Recebeu o sabre de luz

- Mensagens : 149
Data de inscrição : 06/10/2012
Idade : 26
Localização : salvador, BA, Brasil
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












