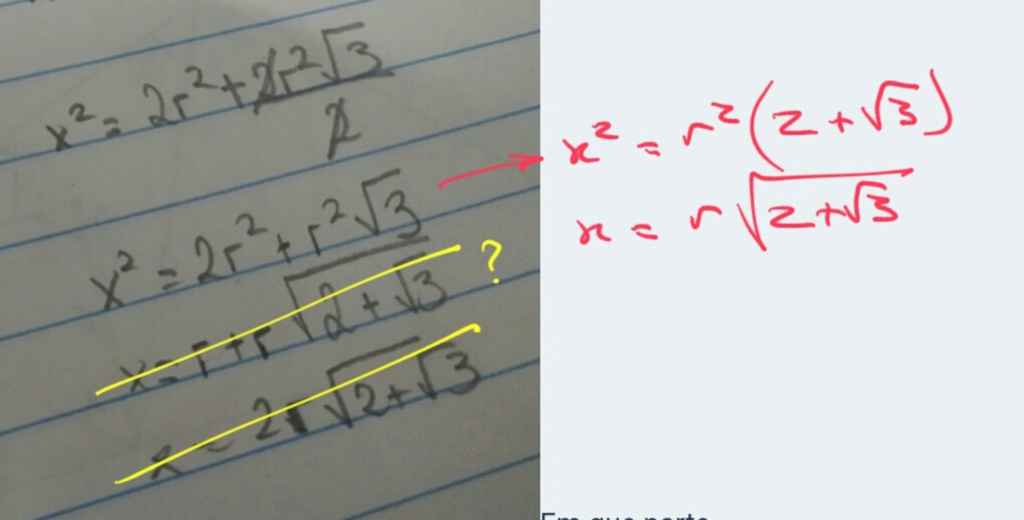EN 1994
+3
Matemathiago
Thomas Prado
Yuri Pantoja
7 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
EN 1994
por Yuri Pantoja Qui 28 Jan 2016, 16:08
A, B e C são três pontos de uma circunferência de raio r, tais que B
pertence ao menor dos arcos de extremidades A e C. AB e BC são iguais aos lados do quadrado e do hexágono regular inscritos na circunferência, respectivamente. A distância entre os pontos A e C é igual a:
pertence ao menor dos arcos de extremidades A e C. AB e BC são iguais aos lados do quadrado e do hexágono regular inscritos na circunferência, respectivamente. A distância entre os pontos A e C é igual a:
Yuri Pantoja- Recebeu o sabre de luz
- Mensagens : 119
Data de inscrição : 26/04/2015
Idade : 26
Localização : Rio Grande-RS-Brasil
Re: EN 1994
por Thomas Prado Qui 28 Jan 2016, 16:21
Alternativas:
\\ a)\ r \\ b)\ r \sqrt {\sqrt{3}+2} \\ c)\ \frac{r}{2} (\sqrt {2}+1) \\ d)\ r \sqrt {\sqrt{5}} \\ e)\ r \frac{\sqrt{3}}{2}
Thomas Prado- Jedi
- Mensagens : 244
Data de inscrição : 18/02/2015
Idade : 25
Localização : S. José dos Campos - SP
Re: EN 1994
por Matemathiago Qui 28 Jan 2016, 16:57
Lado do quadrado = R . Raiz de 2 = AB
Lado do hexágono = R = BC
(BC)² + (AC)² = (AB)²
R² + (AC)² = 2R²
R² = (AC)²
R = AC
Letra "A".
Obs.: Não tenho certeza, aguardemos outra resposta..
Lado do hexágono = R = BC
(BC)² + (AC)² = (AB)²
R² + (AC)² = 2R²
R² = (AC)²
R = AC
Letra "A".
Obs.: Não tenho certeza, aguardemos outra resposta..
Matemathiago- Estrela Dourada
- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
Re: EN 1994
por Elcioschin Qui 28 Jan 2016, 18:41
Faça um desenho em escala e seja O o centro da circunferência.
Ligue O com A, com B e com C ---> OA = OB = OC = r
OAB é triângulo retângulo isósceles (OA = OB e AÔB = 90º) --> O^BA = 45º
OBC é equilátero ---> O^BC = 60º
A^BC = O^BA + O^BC ---> A^BC = 45º + 60º ---> A^BC = 105º ---> O triângulo ABC NÃO é retângulo
Logo você não pode usar Pitágoras em ABC. Use a lei dos Cossenos: AC² = AB² + BC² - 2.AB.BC.cos105º
Ligue O com A, com B e com C ---> OA = OB = OC = r
OAB é triângulo retângulo isósceles (OA = OB e AÔB = 90º) --> O^BA = 45º
OBC é equilátero ---> O^BC = 60º
A^BC = O^BA + O^BC ---> A^BC = 45º + 60º ---> A^BC = 105º ---> O triângulo ABC NÃO é retângulo
Logo você não pode usar Pitágoras em ABC. Use a lei dos Cossenos: AC² = AB² + BC² - 2.AB.BC.cos105º
Elcioschin- Grande Mestre
- Mensagens : 73164
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Re: EN 1994
por Matemathiago Qui 28 Jan 2016, 20:37
Obrigado pela correção Sr. Elcioschin,
O desenho mental que eu fiz me permitiu afirmar que o triângulo era retângulo, mas percebi que o elaborei errado..
O desenho mental que eu fiz me permitiu afirmar que o triângulo era retângulo, mas percebi que o elaborei errado..
Matemathiago- Estrela Dourada
- Mensagens : 1447
Data de inscrição : 16/08/2015
Idade : 24
Localização : Vitória, ES, Brasil
Re: EN 1994
por Medeiros Sex 29 Jan 2016, 16:29
Também, por resultar mais fácil, podemos considerar os ângulos centrais e o fornecido raio r.
AÔB = 90° , BÔC = 60° -----> AÔC = 90° + 60° = 150°
AC² = r² + r² - 2.r².cos150°
O que leva à alternativa (b).
AÔB = 90° , BÔC = 60° -----> AÔC = 90° + 60° = 150°
AC² = r² + r² - 2.r².cos150°
O que leva à alternativa (b).
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Infantes- Recebeu o sabre de luz
- Mensagens : 144
Data de inscrição : 03/03/2019
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: EN 1994
por Medeiros Sáb 30 Mar 2019, 19:51
Raimundo
vc não está errado (a não ser por preguiça, he he), são a mesma resposta em formatos diferentes.
x= r\sqrt{2+\sqrt{3}} \\\\
u^2= 2^2-3=4-3=1 \to u=1\\\\
x=r\left [ \sqrt{\frac{2+1}{2}}+\sqrt{\frac{2-1}{2}} \right ]=r\left [ \frac{\sqrt{3}}{\sqrt{2}}+\frac{1}{\sqrt{2}} \right ] = r \frac{\sqrt{2}}{2} \left ( \sqrt{3} + 1 \right )
__________________________________EDIÇÃO
ou partindo da sua resposta para a das alternativas
x= r \frac{\sqrt{2}}{2} \left (\sqrt{3} + 1 \right ) \\\\
x^2 = r^2 \cdot \frac{1}{2} \left (3 + 1 + 2\sqrt{3} \right ) \to x^2 = r^2 \left (2+\sqrt{3} \right ) \\\\
\therefore x = r \sqrt{2+\sqrt{3}}
vc não está errado (a não ser por preguiça, he he), são a mesma resposta em formatos diferentes.
u^2= 2^2-3=4-3=1 \to u=1\\\\
x=r\left [ \sqrt{\frac{2+1}{2}}+\sqrt{\frac{2-1}{2}} \right ]=r\left [ \frac{\sqrt{3}}{\sqrt{2}}+\frac{1}{\sqrt{2}} \right ] = r \frac{\sqrt{2}}{2} \left ( \sqrt{3} + 1 \right )
__________________________________EDIÇÃO
ou partindo da sua resposta para a das alternativas
x^2 = r^2 \cdot \frac{1}{2} \left (3 + 1 + 2\sqrt{3} \right ) \to x^2 = r^2 \left (2+\sqrt{3} \right ) \\\\
\therefore x = r \sqrt{2+\sqrt{3}}
Última edição por Medeiros em Sáb 30 Mar 2019, 20:51, editado 1 vez(es) (Motivo da edição : acrescentar a Edição)
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Página 1 de 2 • 1, 2
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
