Pontos comuns à uma parábola e uma reta

por Samuel Leite Dom 13 Dez 2015, 01:47

O gráfico da função $f(x)=ax^{_{2}}+bx+c$ cruza dois pontos, comuns à uma reta r. Sendo esses pontos determinados por $\alpha$ e $\beta$ em relação ao eixo das abscissas:

a) Determine a equação da reta r:
b) Determine se ela cruza o ponto determinado por $x=\gamma$ .

Observações:

$\alpha ,\beta ,\gamma$ ∈ $\mathbb{R}$ .

$\alpha \neq \beta\neq \gamma$

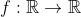
$f:\mathbb{R}\rightarrow \mathbb{R}$

$a,b,c$ ∈ $\mathbb{Z}^{*}$

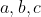CONDIÇÃO: Utilize ambos os pontos ao calcular o coeficiente linear.

Respostas:

por **Elcioschin** Ter 15 Dez 2015, 19:06

Sua resposta poderia ser bem simplificada na 1ª parcela [a.(β + α) + b].x

Sejam P e Q os pontos onde a reta corta a parábola: P[α , f(α)] e Q[β, f(β)]

f(α) = a.α² + b.α + c ---> f(β) = a.β² + b.β + c

Coeficiente angular da reta ---> m = [f(β) - f(α)]/(β - α) ---> m = [(a.β² + b.β + c) - (a.α² + b.α + c)]/(β - α)

m = (a.β² - a.α² + b.β - b.α)/(β - α) ---> m = [a.(β² - α²) - b(β - α)]/(β - α) ---> m = [a.(β + α) + b].x

Equação da reta que passa por P(α, a.α² + b.α + c) e coef. angular m ---> y - yP = m.(x - xP)

Faça as contas e complete

Pontos comuns à uma parábola e uma reta

Pontos comuns à uma parábola e uma reta

Re: Pontos comuns à uma parábola e uma reta

Um fórum livre e democrático.