Determine os pontos críticos
2 participantes
Página 1 de 1
 Determine os pontos críticos
Determine os pontos críticos
Utilizando a derivada, determine os pontos críticos de f(x) = x³ - 3x² + 3x, explicando o que significa cada ponto.
Então, acabei emperrando nessa parte:
Primeiramente tirei a derivada: f'(x) = 3x² - 6x + 3.
Entendo que quando está no ponto crítico, a derivada é zero.
Tirei as raízes: x' = 1 e x'' = 1, logo x' = x'' = 1.
Não consigo achar o ponto máximo e mínimo, não sei como desenvolver esse caso. A partir disso, tentei tirar a derivada de ordem 2.
f''(x) = 6x - 6 >> 6x = 6 >> x = 1. Nesse caso, eu descobri que o ponto de inflexão é igual a 1. Já que se traçarmos o gráfico a gente verifica que muda de sinal, mas continuo sem saber quais são os pontos de máximo e minimo.
Então se alguém puder me ensinar a achar o ponto máximo e mínimo, ficaria muito grato!
Boa Tarde! :face:
Então, acabei emperrando nessa parte:
Primeiramente tirei a derivada: f'(x) = 3x² - 6x + 3.
Entendo que quando está no ponto crítico, a derivada é zero.
Tirei as raízes: x' = 1 e x'' = 1, logo x' = x'' = 1.
Não consigo achar o ponto máximo e mínimo, não sei como desenvolver esse caso. A partir disso, tentei tirar a derivada de ordem 2.
f''(x) = 6x - 6 >> 6x = 6 >> x = 1. Nesse caso, eu descobri que o ponto de inflexão é igual a 1. Já que se traçarmos o gráfico a gente verifica que muda de sinal, mas continuo sem saber quais são os pontos de máximo e minimo.
Então se alguém puder me ensinar a achar o ponto máximo e mínimo, ficaria muito grato!
Boa Tarde! :face:
Prestatie- Padawan

- Mensagens : 54
Data de inscrição : 21/04/2015
Idade : 29
Localização : Paraná
 Re: Determine os pontos críticos
Re: Determine os pontos críticos
A função não tem máximos ou mínimos. f'(x)=0 conduz a um único ponto que é de inflexão.
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Determine os pontos críticos
Re: Determine os pontos críticos
Muito Obrigado Euclides, se for possível, poderia me confirmar se a minha conclusão sobre o ponto de inflexão está correta? Pois sua resposta foi muito valiosa para mim, já que meu professor conserva a parte conceitual e aliás, considera ela tão importante quanto ao próprio cálculo numérico.
Prestatie- Padawan

- Mensagens : 54
Data de inscrição : 21/04/2015
Idade : 29
Localização : Paraná
 Re: Determine os pontos críticos
Re: Determine os pontos críticos
Quando f''(x) > 0 o ponto é de mínimo, quando f''(x) < 0 o ponto é de máximo, se f''(x)=0 é ponto de inflexão.
A função
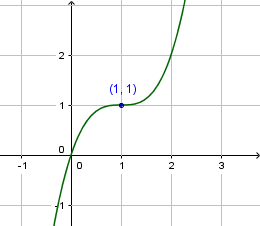
A função

____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Determine os pontos críticos
Re: Determine os pontos críticos
Perfeito! Sua solução esclareceu minha dúvida e consegui terminar a lista de exercícios inclusive. Muito obrigado, tenha uma ótima noite!
Prestatie- Padawan

- Mensagens : 54
Data de inscrição : 21/04/2015
Idade : 29
Localização : Paraná
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












