[Resolvido]Geometria analítica :equação da circunferência
3 participantes
Página 1 de 1
![[Resolvido]Geometria analítica :equação da circunferência Empty](https://2img.net/i/empty.gif) Geometria analítica :equação da circunferência
Geometria analítica :equação da circunferência
Determine a equação geral da circunferência que passa por (-6,0) e é tangente a reta x+y=0 na origem.
Não consegui desenvolver a questão além daqui.
![[Resolvido]Geometria analítica :equação da circunferência Semttulorw](https://2img.net/r/ihimizer/img600/7808/semttulorw.jpg)
A distância entre a origem e o eixo X, chamei de h definida por H(-3,0).(Não pude desenhar pois o desenho ficou muito pequeno).
Então existe uma relação pitagórica entre AC, AH e HC.
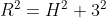
Mas não percebi mais nada a se desenvolvido.Ajuda ?
Não consegui desenvolver a questão além daqui.
![[Resolvido]Geometria analítica :equação da circunferência Semttulorw](https://2img.net/r/ihimizer/img600/7808/semttulorw.jpg)
A distância entre a origem e o eixo X, chamei de h definida por H(-3,0).(Não pude desenhar pois o desenho ficou muito pequeno).
Então existe uma relação pitagórica entre AC, AH e HC.
Mas não percebi mais nada a se desenvolvido.Ajuda ?

DanNoom- Recebeu o sabre de luz

- Mensagens : 172
Data de inscrição : 27/06/2010
Idade : 34
Localização : salvador
![[Resolvido]Geometria analítica :equação da circunferência Empty](https://2img.net/i/empty.gif) Re: [Resolvido]Geometria analítica :equação da circunferência
Re: [Resolvido]Geometria analítica :equação da circunferência
Olá DanNoon,
Se a circunferência passa pelos pontos O( 0, 0 ) e A( - 6, 0 ) então AO é uma corda da circunferência, assim a reta que passa pelo ponto médio dessa corda e é perpendicular à mesma passará pelo centro da circunferência.
Tal reta será x = - 3 como vc já tinha feito.
Temos também que se a circunferência é tangente à reta y = - x então uma reta perpendicular a essa reta passando pelo ponto de tangencia passará pelo centro da circunferência.Assim,
Reta perpendicular à reta y = - x -> y = x
Interseção da reta x = - 3 com a reta y = x -> C( - 3, - 3 )
O raio da circunferência será dado pela distância entre o9s pontos C( - 3, - 3 ) e a origem O( 0, 0 )
d² = (-3-0)² + (-3-0)² = 18
Então a equação da circunferência será dada por:
( x + 3 )² + ( y + 3 )² = 18
x² + 6x + 9 + y² + 6y + 9 = 18
x² + y² + 6x + 6y = 0
Se a circunferência passa pelos pontos O( 0, 0 ) e A( - 6, 0 ) então AO é uma corda da circunferência, assim a reta que passa pelo ponto médio dessa corda e é perpendicular à mesma passará pelo centro da circunferência.
Tal reta será x = - 3 como vc já tinha feito.
Temos também que se a circunferência é tangente à reta y = - x então uma reta perpendicular a essa reta passando pelo ponto de tangencia passará pelo centro da circunferência.Assim,
Reta perpendicular à reta y = - x -> y = x
Interseção da reta x = - 3 com a reta y = x -> C( - 3, - 3 )
O raio da circunferência será dado pela distância entre o9s pontos C( - 3, - 3 ) e a origem O( 0, 0 )
d² = (-3-0)² + (-3-0)² = 18
Então a equação da circunferência será dada por:
( x + 3 )² + ( y + 3 )² = 18
x² + 6x + 9 + y² + 6y + 9 = 18
x² + y² + 6x + 6y = 0

Jose Carlos- Grande Mestre

- Mensagens : 5551
Data de inscrição : 08/07/2009
Idade : 74
Localização : Niterói - RJ
![[Resolvido]Geometria analítica :equação da circunferência Empty](https://2img.net/i/empty.gif) Re: [Resolvido]Geometria analítica :equação da circunferência
Re: [Resolvido]Geometria analítica :equação da circunferência
O centro está na intersecção das perpendiculares:
1) perpendicular a N, ponto médio de AB
2) perpendicular a x+y=0 no ponto B
O raio é a distância BC
![[Resolvido]Geometria analítica :equação da circunferência Trikl](https://2img.net/r/ihimizer/img717/9254/trikl.gif)
1) perpendicular a N, ponto médio de AB
2) perpendicular a x+y=0 no ponto B
O raio é a distância BC
![[Resolvido]Geometria analítica :equação da circunferência Trikl](https://2img.net/r/ihimizer/img717/9254/trikl.gif)
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
![[Resolvido]Geometria analítica :equação da circunferência Empty](https://2img.net/i/empty.gif) Re: [Resolvido]Geometria analítica :equação da circunferência
Re: [Resolvido]Geometria analítica :equação da circunferência
Não tinha notado esse detalhe tão evidente.
Muito obrigado senhores.
Muito obrigado senhores.

DanNoom- Recebeu o sabre de luz

- Mensagens : 172
Data de inscrição : 27/06/2010
Idade : 34
Localização : salvador
 Tópicos semelhantes
Tópicos semelhantes» [Resolvido]Geometria Analitica
» Geometria analítica (RESOLVIDO)
» [Resolvido]Geometria analitica
» [Resolvido]Geometria no triângulo.
» [Resolvido]Geometria Plana
» Geometria analítica (RESOLVIDO)
» [Resolvido]Geometria analitica
» [Resolvido]Geometria no triângulo.
» [Resolvido]Geometria Plana
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos

![[Resolvido]Geometria analítica :equação da circunferência T3Ri1xW](https://i.imgur.com/T3Ri1xW.png)










