(Cesgranrio) Na figura, cada aresta do cubo
4 participantes
Página 1 de 1
(Cesgranrio) Na figura, cada aresta do cubo
por Lauser Sex Ago 07 2015, 21:29
(Cesgranrio) Na figura, cada aresta do cubo mede 3 cm. Prolongando-se uma delas de 5 cm, obtemos o ponto M. A distância, em centímetros, de M ao vértice A é
gabarito b
Meu desenho ficou assim mais ou menos. Eu acredito que a reta da base desse triangulo vai passar quase pelo ponto médio da aresta mais próxima do cubo
Não consegui chegar no resultado
gabarito bMeu desenho ficou assim mais ou menos. Eu acredito que a reta da base desse triangulo vai passar quase pelo ponto médio da aresta mais próxima do cubo
Não consegui chegar no resultado
Lauser- Jedi
- Mensagens : 406
Data de inscrição : 28/07/2015
Idade : 29
Localização : brasilia-DF
Re: (Cesgranrio) Na figura, cada aresta do cubo
por Euclides Sex Ago 07 2015, 21:40
Experimente um triângulo melhor:
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.
Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.
Euclides- Fundador
- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
Re: (Cesgranrio) Na figura, cada aresta do cubo
por Lauser Sex Ago 07 2015, 21:55
Diagonal do quadrado
x^2=3^2+3^2
x^2=18
diagonal da nova figura
DN^2=x^2+8^2
dn^2=18+64
dn=√82
Obrigado Euclides
x^2=3^2+3^2
x^2=18
diagonal da nova figura
DN^2=x^2+8^2
dn^2=18+64
dn=√82
Obrigado Euclides
Lauser- Jedi
- Mensagens : 406
Data de inscrição : 28/07/2015
Idade : 29
Localização : brasilia-DF
Re: (Cesgranrio) Na figura, cada aresta do cubo
por zShake Ter Ago 09 2022, 15:44
Alguém poderia explicar essa ângulo reto? Não consigo o enxergar...Euclides escreveu:Experimente um triângulo melhor:
zShake- Padawan
- Mensagens : 57
Data de inscrição : 10/08/2021
Re: (Cesgranrio) Na figura, cada aresta do cubo
por Elcioschin Ter Ago 09 2022, 17:33
Sejam A, B, C, D os vértices da base inferior, no sentido anti-horário
Sejam E, F, G, H vértices da base superior, no sentido anti-horário, com E acima de A
O segmento de reta MH é perpendicular ao lado EH
Logo, MH é perpendicular á face ADHE, no ponto H
Como consequência, MH é perpendicular à diagonal AH, no mesmo ponto H
Aproveito para colocar a outra solução:
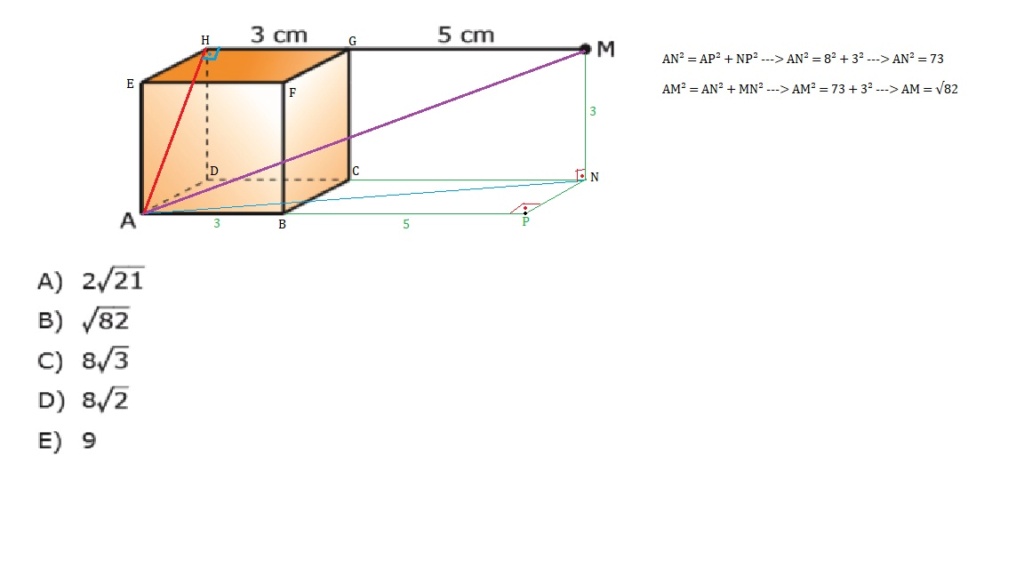
Sejam E, F, G, H vértices da base superior, no sentido anti-horário, com E acima de A
O segmento de reta MH é perpendicular ao lado EH
Logo, MH é perpendicular á face ADHE, no ponto H
Como consequência, MH é perpendicular à diagonal AH, no mesmo ponto H
Aproveito para colocar a outra solução:
Elcioschin- Grande Mestre
- Mensagens : 71683
Data de inscrição : 15/09/2009
Idade : 77
Localização : Santos/SP
zShake gosta desta mensagem
Tópicos semelhantes» Um cubo de aresta a tem em cada vértice o cen
» (Esal-MG) Em um cubo de aresta a
» Medida da aresta do cubo
» Cubo de aresta
» Aresta de um cubo.
» (Esal-MG) Em um cubo de aresta a
» Medida da aresta do cubo
» Cubo de aresta
» Aresta de um cubo.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
