(Escola Naval - 2010) Estática

A figura abaixo mostra uma barra uniforme e homogênea de peso e comprimento , em repouso sobre uma superfície horizontal. A barra está apoiada, sem atrito, ao topo de uma coluna vertical de altura 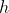, fazendo um ângulo de 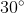com a vertical. Um bloco de peso está pendurado a uma distância da extremidade inferior da barra. Se a barra está na iminência de deslizar, a expressão do módulo da força de atrito entre a sua extremidade inferior e a superfície horizontal é



(A)

(B)

(C)

(D)

(E)

Sejam:

A = ponto onde a escada toca a aparede
B = ponto onde a escada toca o chão
C = ponto de escada onde está dependurado o peso
M = ponto médio da escada
O = ponto de contato entre a parede e o chão

AM = BM = L/2
AC = AB - BC ----> AC = L - L/3 ----> AC = 2L/3

Forças atuantes (sem contar o ponto A):

Peso P da escada atuando no ponto M (vertical para baixo)
Peso P/2 atuando no ponto C (vertical para baixo)
Reação normal N do solo sobre a escada (ponto B, vertical para cima)
Força de atrito atuando no ponto B (horizontal para a esquerda)

N = P + P/2 ----> N = 3*P/2

Momento das forças em relação ao ponto A: M(P) + M(P/2) + M(F) = M(N)

P*(AM*cos60º) + (P/2)*(AC*cos60º) + F*h = N*(AB*cos60º)

P*(L/2)*cos60º + (P/2)*(2L/3)*cos60º + F*h = (3P/2)*(L*cos60º)

PL/4 + PL/6 + F*h = 3PL/4 ----> F*h = PL/4 ----> F = PL/4h ----> Alternativa A

Respostas curiosas da alternativas levando em conta que h = L*cos30º ----> h = L*\/3/2

Substituindo h nas alternativas o valor de F o valor de F dependerá apenas de P. Neste caso a alternativa A deveria estar assim ----> F = P*\/3/6

Concordo com a solução teórica da questão, mas há um erro na última linha:
Se F*h = 3PL/4 - PL/4 - PL/6, então F*h = PL/3 e não PL/4!
Inclusive isto tora a questão sem alternativas corretas
O mestre Elcioschin ou algum dos monitores podem me confirmar isso?
Obrigado

Bruno

Concordo integralmente com suas observações: F = PL/3h

Não entendi porque a medida de AM vale L/2, visto que A não é o termino da barra, levando em conta que a medida total da barra vale L.

Veja o que eu escrevi:: "M = ponto médio da escada"


Se a escada AB tem comprimento L, isto é, se AB = L, o ponto médio M dela dista L/2 de ambas as extremidades: AM = BM = L/2


O ponto M é o centro de gravidade da escada, onde atua a força peso da mesma.

Desculpa a insistência professor, porém minha dúvida ainda continua. Concordo que do ponto M à ambas extremidades o comprimento vai ser L/2, porém, A(que é o ponto de contato com a parede) não é uma extremidade ao meu ver. Desde já muito obrigado

Gierson

Não há o que desculpar meu caro: eu é que não tinha entendido sua dúvida, por não ter olhado o desenho com atenção. Agora entendo e posso dar a minha opinião

Acho que existe erro no desenho: não existe aquele prolongamento além da parede, isto é, a parte superior da escada termina exatamente na parede.

Se não fosse assim o problema não teria solução, já que não consta no enunciado o valor do comprimento acima da parede.

O que você acha a respeito?

Acho que gastei horas tentando arrumar jeitos de calcular aquela parte acima do ponto A usando o ângulo de 30º e etc, não me saia da cabeça que todo comprimento da barra valia L, logo os comprimentos abaixo do ponto A tinham que ser diferentes, questão mal formulada, não é mesmo?

Certamente meu caro: muito mal formulada.