No plano cartesiano, duas retas r e s
2 participantes
Página 1 de 1
No plano cartesiano, duas retas r e s
por paulooctavio Qui 28 maio 2015, 23:48
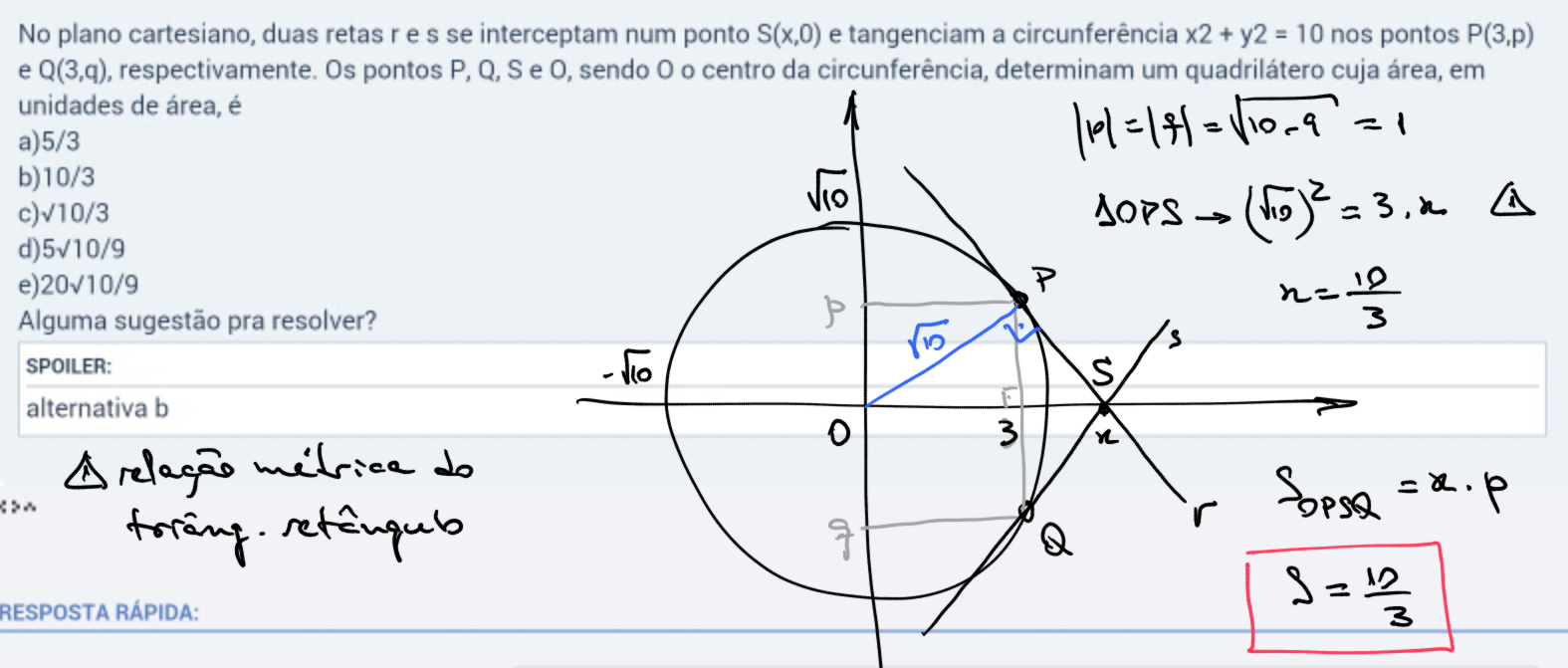
No plano cartesiano, duas retas r e s se interceptam num ponto S(x,0) e tangenciam a circunferência x2 + y2 = 10 nos pontos P(3,p) e Q(3,q), respectivamente. Os pontos P, Q, S e O, sendo O o centro da circunferência, determinam um quadrilátero cuja área, em unidades de área, é
a)5/3
b)10/3
c)√10/3
d)5√10/9
e)20√10/9
Alguma sugestão pra resolver?
a)5/3
b)10/3
c)√10/3
d)5√10/9
e)20√10/9
Alguma sugestão pra resolver?
- Spoiler:
- alternativa b
paulooctavio- Iniciante
- Mensagens : 31
Data de inscrição : 22/03/2015
Idade : 26
Localização : Belo Horizonte, Minas Gerais, Brasil
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Tópicos semelhantes» Area entre duas retas no plano cartesiano
» Plano cartesiano + retas
» (UFJF - 2009) - Pontos e Retas no Plano Cartesiano.
» Quadrado, plano cartesiano e retas
» Pontos e retas no Plano Cartesiano
» Plano cartesiano + retas
» (UFJF - 2009) - Pontos e Retas no Plano Cartesiano.
» Quadrado, plano cartesiano e retas
» Pontos e retas no Plano Cartesiano
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos
