áreas de superfícies....

Relembrando a primeira mensagem :

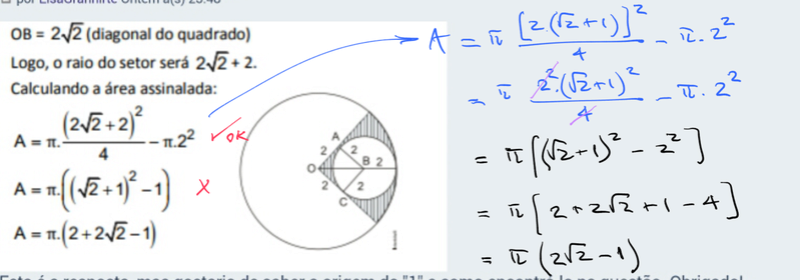
Uma circunferência de raio 2 tangencia outra e dois de seus raios, conforme figura seguinte.

O valor da área hachurada é
a)  2π √2 b)  3π (√2 – 1) c)  2π (√2 – 3) d)  π (2√2 – 1) << gabarito

Eu fiz ao quadrado o errezão R² ( 2 + 2V2) ²=  (2 + 2v2) ( 2 + 2v2) = 8 + 4V2 + 4V2 + 4 = 8 + 4 + 8V2 = 12 + 8V2 ,  mas ai ta difícil kkkkkkk , então quer dizer que ficou 1/3 pi r² . R² ????

Cara, você está muito desatento:

S = (1/4).pi.R² ---> Você esqueceu de dividir por 4 !!!!

conseguiiii , amém !           é que ele fez (1/4) pi. R²(2+2v2 + 1) era para ele ter colocado 1/4 piR² = ( 2 + 2v2 + 1) = 3 + 2V2 ,   eu estava multiplicando o do parênteses pelo errezinho ao quadrado , só que o do parênteses era o resultado da conta 1/4 PIR² ^^

Não, meu caro Kowalski, o que fiz foi:

1) no cálculo de R, deixei o 2 em evidência ---> R = 2√2 + 2 = 2.(√2 +1)

2) para calcular R², apliquei a propriedade: (a.b)² = a².b². Ou seja, R² = 2².(√2 + 1)².
....E (√2 + 1)² = (2 + 2√2 + 1) = (2√2 + 3)

Tudo isto ficou MUITO BEM indicado nos meus escritos.
Cá entre nós, parece que você não faz o mínimo esforço para chegar a um resultado, parece que espera tudo pronto, mastigado e acabado. Ou então, tem muito pouca auto-estima, o que lhe acarreta medo de tentar e errar. Porque custo a crer que alguém no Ensino Médio tenha a dificuldade que você apresenta nas coisas mais comezinhas.
Grande parte do aprendizado é tentativa e erro. Tente, arrisque. Não precisa ter medo (do quê?). Errou? Pense "e se..." e tente novamente. Com o tempo, as peças se encaixam como num quebra-cabeças.

Abraço.

O raio é igual a 2 + 2√2 certo?
O valor da área colorida é (2 + 2√2 ) - pi.R² dividido por 4, certo?
Como deu 1, em pi.R², se o raio vale 4?

Esta é a resposta, mas gostaria de saber a origem do "1" e como encontrá-lo na questão. Obrigado!

Kowalski escreveu:Uma circunferência de raio 2 tangencia outra e dois de seus raios, conforme figura seguinte.

O valor da área hachurada é
a)  2π √2 b)  3π (√2 – 1) c)  2π (√2 – 3) d)  π (2√2 – 1) << gabarito

Eu tentei resolver igual a postagem da ElsaGranhirte, mas a resposta saiu igual o gabarito do Kowalski. Me corrigir se estiver errado. Obrigado.

Você está certo, Merion.

Elsa, você está cometendo erros de aritmética quanto à propriedade distributiva nas passagens; veja: