Triangulo - Baricentro
5 participantes
Página 1 de 2
Página 1 de 2 • 1, 2 
Triangulo - Baricentro
por jaques104 Sex 13 Mar 2015, 10:04
Na figura, D é o ponto médio do lado AB e DE é paralelo a BC. Se AC = 54 cm, calcule a medida do segmento GB.
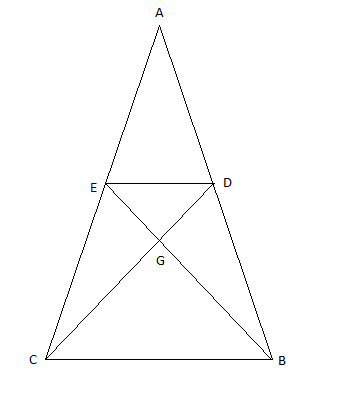
resposta: 18cm
resposta: 18cm
jaques104- Recebeu o sabre de luz
- Mensagens : 149
Data de inscrição : 06/10/2012
Idade : 26
Localização : salvador, BA, Brasil
Re: Triangulo - Baricentro
por Medeiros Sáb 14 Mar 2015, 16:26
O enunciado, do qual a figura faz parte, está incompleto.
A única forma de resultar no valor do gabarito, GB=18 cm é se o ângulo ^B do triângulo ABC for reto. Então EB = EC = EA = 27 cm.
BE e CD são medianas, logo o ponto G é baricentro e GB = (2/3).EB.
A única forma de resultar no valor do gabarito, GB=18 cm é se o ângulo ^B do triângulo ABC for reto. Então EB = EC = EA = 27 cm.
BE e CD são medianas, logo o ponto G é baricentro e GB = (2/3).EB.
Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Triangulo - Baricentro
por raimundo pereira Sáb 14 Mar 2015, 17:24
xxxxxx
Última edição por raimundo pereira em Sáb 14 Mar 2015, 19:15, editado 1 vez(es)
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Triangulo - Baricentro
por raimundo pereira Sáb 14 Mar 2015, 18:05
xxxxx
Última edição por raimundo pereira em Sáb 14 Mar 2015, 19:16, editado 1 vez(es)
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Triangulo - Baricentro
por Medeiros Sáb 14 Mar 2015, 18:18
Desculpe, Raimundo, mas discordo.
o enunciado informa apenas que AC=54 cm, o ponto médio de AB e o paralelismo DE//BC, nada mais.
o enunciado informa apenas que AC=54 cm, o ponto médio de AB e o paralelismo DE//BC, nada mais.
Última edição por Medeiros em Sáb 14 Mar 2015, 19:33, editado 1 vez(es) (Motivo da edição : eliminar redundância.)
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Triangulo - Baricentro
por raimundo pereira Sáb 14 Mar 2015, 19:14
Tudo verdade . Isso não foi distração , foi "mancada". Acho que a cabeça esta a mil e viu um retângulo. Sorry!
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Triangulo - Baricentro
por Medeiros Sáb 14 Mar 2015, 19:46
Entendo que o problema, de fato, está mal posto. E para a gente, que sempre procura encontrar uma saída para a questão, isso funciona como armadilha que nos seduz até a distração.
Medeiros- Grupo
Velhos amigos do Fórum - Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
Re: Triangulo - Baricentro
por raimundo pereira Sáb 14 Mar 2015, 19:46
Postando o desenho com o 1° cometário do Medeiros.
raimundo pereira- Grupo
Velhos amigos do Fórum - Mensagens : 6114
Data de inscrição : 13/06/2012
Idade : 83
Localização : Rio de Janeiro
Re: Triangulo - Baricentro
por j3ck.tekila Qua 06 Nov 2019, 20:15
Olá colegas, ainda estão por aí??
Estou com essa questão no meu material e realmente o triângulo ABC é retângulo...
Eu gostaria de entender por que o triângulo precisa ser retângulo para essa questão ser possível... Não estou enxergando a diferença que ele faz. Se puderem me ajudar eu agradeço!!
Estou com essa questão no meu material e realmente o triângulo ABC é retângulo...
Eu gostaria de entender por que o triângulo precisa ser retângulo para essa questão ser possível... Não estou enxergando a diferença que ele faz. Se puderem me ajudar eu agradeço!!
j3ck.tekila- Iniciante
- Mensagens : 2
Data de inscrição : 04/07/2015
Idade : 41
Localização : santos sp brasil
Re: Triangulo - Baricentro
por Elcioschin Qua 06 Nov 2019, 21:03
Sendo ABC retângulo em B, AC é a hipotenusa
E é o ponto médio da hipotenusa: AC = 54 ---> AE = CE = 27
Todo triângulo retângulo é inscritível numa semi-circunferência, tendo a hipotenusa como diâmetro:
R = 27 ---> Neste caso BE = 27
BE é a mediana relativa à hipotensa AC, logo G é o baricentro do triângulo;
O baricentro divide a mediana na razão 2 para 1, isto é:
BG = 2.EG ---> BG + EG = 27 ---> 2.EG + EG = 27 ---> EG = 9 ---> BG = 18
E é o ponto médio da hipotenusa: AC = 54 ---> AE = CE = 27
Todo triângulo retângulo é inscritível numa semi-circunferência, tendo a hipotenusa como diâmetro:
R = 27 ---> Neste caso BE = 27
BE é a mediana relativa à hipotensa AC, logo G é o baricentro do triângulo;
O baricentro divide a mediana na razão 2 para 1, isto é:
BG = 2.EG ---> BG + EG = 27 ---> 2.EG + EG = 27 ---> EG = 9 ---> BG = 18
Elcioschin- Grande Mestre
- Mensagens : 73163
Data de inscrição : 15/09/2009
Idade : 78
Localização : Santos/SP
Página 1 de 2 • 1, 2
Tópicos semelhantes» Baricentro do triangulo ABC
» Baricentro do triangulo
» Baricentro do triângulo
» o baricentro do triangulo ABC
» Triângulo - (baricentro)
» Baricentro do triangulo
» Baricentro do triângulo
» o baricentro do triangulo ABC
» Triângulo - (baricentro)
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos
