Resto de uma divisão

Achar o resto da divisão do número :

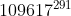
Pelo divisor 9
Resposta:
Zero

Só usando módulo mesmo:

http://www.wolframalpha.com/input/?i=109617%5E291+%28mod+9%29

Re: Pergunta sobre resto
por Chris » Sex 27 Ago, 2010 16:23

Balanar, você lembra das condições de divisibilidade do 3?

Bom, a idéia é que, se a soma dos algarismos de um número é divísivel por 3, o mesmo é divisível por 3. E pode se observar isso na base dessa potência (109617):

1 + 0 + 9 + 6 + 1 + 7 = 24 (que é divisível por 3).

Portanto, o número 109617 pe divisível por 3, logo é 3 vezes alguma coisa (de fato 109617 = 3 * 36539).

Portanto, se elevarmos esse número a 291, teremos dozentos e noventa e uma vez o 3 aparecendo. Como 3*3 é 9, teremos o 9 aparecendo algumas vezes. Portanto, o número é divísivel por 9. Então o resto é zero.