Colinearidade
2 participantes
Página 1 de 1
 Colinearidade
Colinearidade
Verificar se os pontos são colineares:
A = (2, 1, -1)
B = (3, -1, 0)
C = (1, 0, 4)
Procurei uma maneira alternativa de resolver esse tipo de problema sem recorre ao uso de matrizes e achei a seguinte fórmula: (xC - xA)/(xB - xC) = (yC - yA)/(yB - yC). Se a igualdade for verdadeira os pontos são colineares mas eu fiquei em dúvida sobre de onde surge essa fórmula.
Obrigado desde já!
A = (2, 1, -1)
B = (3, -1, 0)
C = (1, 0, 4)
Procurei uma maneira alternativa de resolver esse tipo de problema sem recorre ao uso de matrizes e achei a seguinte fórmula: (xC - xA)/(xB - xC) = (yC - yA)/(yB - yC). Se a igualdade for verdadeira os pontos são colineares mas eu fiquei em dúvida sobre de onde surge essa fórmula.
Obrigado desde já!
ViniciusAlmeida12- Mestre Jedi

- Mensagens : 725
Data de inscrição : 02/02/2013
Idade : 28
Localização : Bahia
 Re: Colinearidade
Re: Colinearidade
é pura aplicação de trigonometria.
Por exemplo, temos os pontos no plano:

Podemos dizer então:
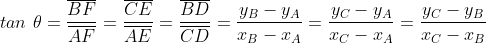
Isto é, se ajeitarmos a equação, temos então:
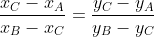
E está correto sim.
Contudo, estamos lidando com 3 coordenadas, creio que será dificil deste meio. Seria melhor pela equação da reta no espaço.
Se formos pela equação, temos:
Vetor AB=(1, -2, 1)
A equação da reta é então:
r: (2, 1, -1)+t(1, -2, 1)
Agora, queremos saber se C pertence, então temos:
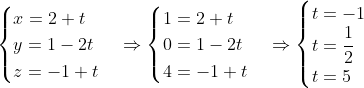
Como os valores de t obtidos em cada caso são diferentes, concluimos que não são colineares.
Outra maneira é usar determinante. Se o determinante der 0, são colineares.
![M=\begin{bmatrix}2 & 1 & -1 \\ 3 & -1 & 0 \\ 1 & 0 & 4 \end{bmatrix} \Rightarrow det[M]=-21](https://latex.codecogs.com/gif.latex?M=\begin{bmatrix}2&space;&&space;1&space;&&space;-1&space;\\&space;3&space;&&space;-1&space;&&space;0&space;\\&space;1&space;&&space;0&space;&&space;4&space;\end{bmatrix}&space;\Rightarrow&space;det[M]=-21)
Deste modo, não são colineares. E a área do triângulo será 21 unidades ao quadrado.
Estão aqui os pontos no espaço:

Por exemplo, temos os pontos no plano:

Podemos dizer então:
Isto é, se ajeitarmos a equação, temos então:
E está correto sim.
Contudo, estamos lidando com 3 coordenadas, creio que será dificil deste meio. Seria melhor pela equação da reta no espaço.
Se formos pela equação, temos:
Vetor AB=(1, -2, 1)
A equação da reta é então:
r: (2, 1, -1)+t(1, -2, 1)
Agora, queremos saber se C pertence, então temos:
Como os valores de t obtidos em cada caso são diferentes, concluimos que não são colineares.
Outra maneira é usar determinante. Se o determinante der 0, são colineares.
Deste modo, não são colineares. E a área do triângulo será 21 unidades ao quadrado.
Estão aqui os pontos no espaço:

____________________________________________
← → ↛  ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥
 ⇌ ⇔ ⇐ ⇒ ⇏ ➥
⇌ ⇔ ⇐ ⇒ ⇏ ➥⁰ ¹ ² ³ ⁴ ⁵ ⁶ ⁷ ⁸ ⁹ ⁺ ⁻ ⁼ ⁽ ⁾ º ª ⁿ ⁱ
₀ ₁ ₂ ₃ ₄ ₅ ₆ ₇ ₈ ₉ ₊ ₋ ₌ ₍ ₎ ₐ ₑ ₒ ₓ ₔ
∴ ≈ ≠ ≡ ≢ ≤ ≥ × ± ∓ ∑ ∏ √ ∛ ∜ ∝ ∞
∀ ∃ ∈ ∉ ⊂ ⊄ ⋂ ⋃ ∧ ∨ ℝ ℕ ℚ ℤ ℂ
⊥ ║ ∡ ∠ ∢ ⊿ △ □ ▭ ◊ ○ ∆ ◦ ⊙ ⊗ ◈
Αα Ββ Γγ Δδ Εε Ζζ Ηη Θθ Ιι Κκ Λλ Μμ Νν Ξξ Οο Ππ Ρρ Σσς Ττ Υυ Φφ Χχ Ψψ Ωω ϑ ϒ ϖ ƒ ij ℓ
∫ ∬ ∭ ∳ ∂ ∇
 ℛ ℜ ℰ ℳ ℊ ℒ
ℛ ℜ ℰ ℳ ℊ ℒ
Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Tópicos semelhantes
Tópicos semelhantes» Colinearidade
» Conjunto de pontos, colinearidade
» Colinearidade - FME
» Colinearidade, coplanaridade e dependência l
» Demostração de Colinearidade e Equação de Reta.
» Conjunto de pontos, colinearidade
» Colinearidade - FME
» Colinearidade, coplanaridade e dependência l
» Demostração de Colinearidade e Equação de Reta.
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












