Desigualdade das Médias

Vou fazer aqui mesmo:
Primeiro, é fundamental que você saiba que Média aritmética é maior ou igual à média geométrica, e serão iguais se, e somente se x1=x2=x3...=xn
Vamos lá:


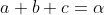
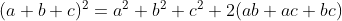
Então, agora, trabalharemos as desigualdades das médias: 




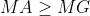
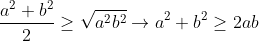
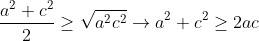
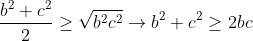
Somando todas as equações

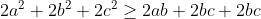
depois disso adicionamos a²+b²+c² aos dois lados de desigualdade.




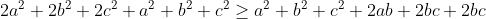
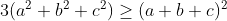
agora observe que:
1. Se a=b=c, serão ambos membros iguais;
2. O 3 equivale a n, portanto , varia em número conforme os termos dentro do parênteses;
3. É válida qualquer que seja o número de variáveis, então vou deixá-la válida não só para esse exercício em específico.



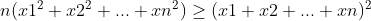
Realmente espero que gostem.

Observação:
O que mais gosto neste fórum é que tem muitos colegas às 12 h de domingo de carnaval, estudando juntos. Em pouquíssimos lugares encontra-se pessoas assim.
Abraços.

Olá, Pedro! Gostaria de fazer algumas observações.
Como você já deve saber, provar para o caso n = 3 não significa que funcione para um caso geral n mesmo.
Note também que a média aritmética de a e b é (a+b)/2 e não (a²+b²)/2, como você fez.
Sua última expressão escrita em latex também está incorreta e incoerente.

1.Eu fiz a prova para o n número de variáveis, e está correto, só não quis pôr aqui porque eu estava resolvendo aquele exercício;
2.A média aritmética de (a+b)/2 é quando se considera a média de a e b, mas é (a²+b²)/2 quando eu considero a média aritmética a² e b²;
3.Explique-me por que ela está incorreta e incoerente, até porque nada mais é que a generalização da anterior.

1. Não, você fez a "prova" o número 3 de variáveis. E a prova não está nem bem definida, pois deveria ter começa um um enunciado como: "Sejam x1, x2, ..., xn números positivos. Então...".
Outro fator crucial é que se você quer provar uma coisa, não pode começar a demonstração partindo dela. Você já iniciou a demonstração escrevendo que Ma >= Mg e isso já invalida completamente a demonstração. Você queria provar que aquilo era verdade e já começou partindo que era? Dessa forma é possível partir de absurdos e chegar em verdades, veja:
2 = 3 I
3 = 2 II
E eu posso somar membro a membro I + II:
5 = 5
Parti de uma mentira e cheguei em uma verdade. Bem, acho que já ficou claro que não se pode começar a provar algo já assumindo que isso é verdade, nem faria sentido.

2) Neste caso ok, só não entendi porque partiu de quadrados. Neste pedaço está correto, mas interfere no item a seguir.

3) Está incoerente com o que você queria provar pois primeiro o que você escreveu não são as expressões das médias, mas sim algo que você obteve manipulando desigualdades de um caso particular (n = 3), e generalizando pra n.
Escrever que Ma >= Mg seria:
(x1 + x2 + ... + xn)/n >= (x1*x2*...*xn)^(1/n)

Eu já considerei verdade o fato de Ma>=Mg, pois é feita outra demonstração para provar isso, então tomei a decisão de omitir essa parte, além de que não achei necessário que, para a compreensão da desigualdade,  eu começasse com um enunciado como o que você citou.
Também, algo que você deveria ter levado em consideração, eu não tive, a princípio, o objetivo de demonstrá-la para todo e qualquer valor de n, somente para 3, conforme pedia o exercício, por isso acrescentei as observações ao final.

O enunciado é fundamental para a prova. Se o radicando der negativo já deixa de valer tudo, por isso o enunciado é essencial.
Em nenhum momento você disse que era um exercício seu que pedia a demonstração para o caso n = 3. Tudo ficou claro como se tivesse mostrado pra 3 e admitido válido para n.
Mas ok, é isso aí, é legal tentar se preocupar em demonstrar. Se quiser mandar seu email por PM depois te mando um livro que tem a demonstração da desiguldade entre as 4 médias.

Acontece que não fui eu quem pôs ela no c.q.d, eu estava demonstrando para um exercício específico:
Sabendo que a+b+c=1, demonstre que a²+b²+c²>=1/3.
Vou refazê-la (até porque já retiraram daquela seção).
Qual o nome do livro? eu tenho um só sobre fatorações e desigualdades, mas se esse teu tiver algo além, eu ficaria muito grato.

Se é só sobre fatoração e desigualdades, provavelmente é o Tópicos de Matemática mesmo.

É o mesmo. Boa noite.