Conjuntos - Diferença e complementar
2 participantes
PiR2 :: Matemática :: Álgebra
Página 2 de 2
Página 2 de 2 •  1, 2
1, 2
 Conjuntos - Diferença e complementar
Conjuntos - Diferença e complementar
Relembrando a primeira mensagem :
"Gostaria que me explicassem as seguintes propriedades.
1ª) Complementar do complementar do conjunto a = A para todo A ⊂ U ( O que é complementar do complementar?)
2ª) Se A ⊂, então B^C ⊂ A^C ( se um conjunto está contido em outro, seu complementar contém o complementar desse outro [ não entendi, como assim]). Escrevendo de outra forma:
"Gostaria que me explicassem as seguintes propriedades.
1ª) Complementar do complementar do conjunto a = A para todo A ⊂ U ( O que é complementar do complementar?)
2ª) Se A ⊂, então B^C ⊂ A^C ( se um conjunto está contido em outro, seu complementar contém o complementar desse outro [ não entendi, como assim]). Escrevendo de outra forma:
A ⊂ B → B^C ⊂ A^C ( Não entendi também)"
P.S:Retirado da apostila que tirei fotocópia.
Convidado- Convidado
 Re: Conjuntos - Diferença e complementar
Re: Conjuntos - Diferença e complementar
Licença pessoal,
José, sua duvida seria provar isso:
A⊂B → CB(CAB)=A
Se sim, eu acho que tambem poderia fazer dessa forma:
Da definição de Complementar:
Se A⊂B, então CAB= B-A , isto é, X∈B e X∈≠A
Neste caso, CB(CAB) significa que X∈B e X∈≠CAB → X∈B e X∈≠B-A → X∈B e X∈A → X∈AՈB → Como A⊂B → X∈A
Leia (∈≠) como "não pertence". Não encontrei o simbolo...
Voce esta se referindo a isso?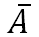 .Se sim, isto é, se não me engano, o complementar de A em relação ao conjunto universo, ou seja, CAU=U-A= X∈U e X∈≠A
.Se sim, isto é, se não me engano, o complementar de A em relação ao conjunto universo, ou seja, CAU=U-A= X∈U e X∈≠A
José, sua duvida seria provar isso:
A⊂B → CB(CAB)=A
Se sim, eu acho que tambem poderia fazer dessa forma:
Da definição de Complementar:
Se A⊂B, então CAB= B-A , isto é, X∈B e X∈≠A
Neste caso, CB(CAB) significa que X∈B e X∈≠CAB → X∈B e X∈≠B-A → X∈B e X∈A → X∈AՈB → Como A⊂B → X∈A
Leia (∈≠) como "não pertence". Não encontrei o simbolo...
José Ricardo dos Santos escreveu:
Hoshyminiag, como eu leio aquele A com uma linha em cima e o que é esse complementar fora dos parênteses?
Voce esta se referindo a isso?
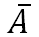 .Se sim, isto é, se não me engano, o complementar de A em relação ao conjunto universo, ou seja, CAU=U-A= X∈U e X∈≠A
.Se sim, isto é, se não me engano, o complementar de A em relação ao conjunto universo, ou seja, CAU=U-A= X∈U e X∈≠AÚltima edição por L.Lawliet em Qui 18 Dez 2014, 14:55, editado 1 vez(es)
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
 Re: Conjuntos - Diferença e complementar
Re: Conjuntos - Diferença e complementar
Muito obrigado gente, mas ainda me resta dúvidas...
L.Lawliet escreveu:Neste caso, CB(CAB) significa que X∈B e X∈≠CAB → X∈B e X∈≠B-A → X∈B e X∈A → X∈AՈB → Como A⊂B → X∈A
CB(CAB), não sei como se lê isso Lawliet.
Convidado- Convidado
 Re: Conjuntos - Diferença e complementar
Re: Conjuntos - Diferença e complementar
José, imagino que CB(CAB) seja lido como "complementar do complementar de A em relação a B". Mas , da propriedade CB(CAB)=A. , voce poderia ler diretamente "A".
Qualquer coisa, dê uma lida na teoria novamente. Tem esse material:
http://projetomedicina.com.br/site/attachments/article/331/matematica_conjuntos_teoria_exercicios.pdf
Qualquer coisa, dê uma lida na teoria novamente. Tem esse material:
http://projetomedicina.com.br/site/attachments/article/331/matematica_conjuntos_teoria_exercicios.pdf
L.Lawliet- Mestre Jedi

- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Página 2 de 2 •  1, 2
1, 2
 Tópicos semelhantes
Tópicos semelhantes» CONJUNTOS - Diferença e Complementar
» Complementar de A em B(Conjuntos).
» Complementar da relação de conjuntos
» (EsPCEx) (União + Intersecção + Complementar) ---> Conjuntos
» Diferença de dois conjuntos
» Complementar de A em B(Conjuntos).
» Complementar da relação de conjuntos
» (EsPCEx) (União + Intersecção + Complementar) ---> Conjuntos
» Diferença de dois conjuntos
PiR2 :: Matemática :: Álgebra
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












