Domínio da função
3 participantes
PiR2 :: Matemática :: Álgebra
Página 2 de 2
Página 2 de 2 • 
1, 2
Domínio da função
por Pietro di Bernadone Sáb 22 Nov 2014, 20:38
Relembrando a primeira mensagem :
Seja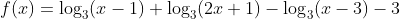
e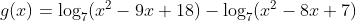 
. Qual o domínio da função 
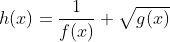em forma de intervalo?
Seja
Pietro di Bernadone- Grupo
Velhos amigos do Fórum
- Mensagens : 1341
Data de inscrição : 05/03/2010
Idade : 34
Localização : Rio de Janeiro
Re: Domínio da função
por L.Lawliet Qui 27 Nov 2014, 03:21
Licença galera.
Pietro di Bernadone, eu acho que faz assim:
Estabelecendo a condição de existencia. Teriamos:
● x-1 >0 → x > 1
● 2x+1 >0 → x> -1/2
● x-3>0 → x > 3
● x² - 9x +18 >0 → x ∈ (-oo;3) ∪ (6;oo)
● x² - 8x + 7 > 0 → x ∈ (-oo;1) ∪ (7;oo)
Fazendo a interseção, teriamos: x > 7
■ 1/ƒ(x) → ƒ(x)≠0
+log_{3}(2x+1)-log_{3}(x-3)\neq&space;0\\\\log_{3}\left&space;[&space;\frac{(x-1)(2x+1)}{x-3}&space;\right&space;]\neq&space;0\\\\\\\frac{(x-1)(2x+1)}{x-3}&space;\right&space;]\neq&space;1\\\\\frac{x^2-x+1}{x-3}\neq&space;0 "\\log_{3}(x-1)+log_{3}(2x+1)-log_{3}(x-3)\neq 0\\\\log_{3}\left [ \frac{(x-1)(2x+1)}{x-3} \right ]\neq 0\\\\\\\frac{(x-1)(2x+1)}{x-3} \right ]\neq 1\\\\\frac{x^2-x+1}{x-3}\neq 0")
A função do numerador apresenta raizes complexas e pela condição de existencia, "x" é diferente de (3).
■ Para √(g(x) ) → g(x)≥0.
-log_{7}(x^2-8x+7)\geqslant&space;0\\\\log_{7}\left&space;[&space;\frac{x^2-9x+18}{x^2-8x+7}&space;\right&space;]\geqslant&space;0\\\\\\\frac{x^2-9x+18}{x^2-8x+7}&space;\right&space;]\geqslant&space;1\\\\\\\frac{11-x}{x^2-8x+7}\geqslant&space;0 "\\log_{7}(x^2-9x+18)-log_{7}(x^2-8x+7)\geqslant 0\\\\log_{7}\left [ \frac{x^2-9x+18}{x^2-8x+7} \right ]\geqslant 0\\\\\\\frac{x^2-9x+18}{x^2-8x+7} \right ]\geqslant 1\\\\\\\frac{11-x}{x^2-8x+7}\geqslant 0")
x ∈ (-oo;1) ∪ (7;11]
Fazendo a interseção com a condição de existencia, teriamos:
Xfinal ∈ (7;11]
Pietro di Bernadone, eu acho que faz assim:
Estabelecendo a condição de existencia. Teriamos:
● x-1 >0 → x > 1
● 2x+1 >0 → x> -1/2
● x-3>0 → x > 3
● x² - 9x +18 >0 → x ∈ (-oo;3) ∪ (6;oo)
● x² - 8x + 7 > 0 → x ∈ (-oo;1) ∪ (7;oo)
Fazendo a interseção, teriamos: x > 7
■ 1/ƒ(x) → ƒ(x)≠0
A função do numerador apresenta raizes complexas e pela condição de existencia, "x" é diferente de (3).
■ Para √(g(x) ) → g(x)≥0.
x ∈ (-oo;1) ∪ (7;11]
Fazendo a interseção com a condição de existencia, teriamos:
Xfinal ∈ (7;11]
- Propriedades:
L.Lawliet- Mestre Jedi
- Mensagens : 797
Data de inscrição : 30/10/2013
Idade : 28
Localização : Brasil
Página 2 de 2 • 1, 2
Tópicos semelhantes» [Função] Domínio de uma função de grau 3.
» Domínio da função
» dominio função
» Domínio da função
» Domínio da função!
» Domínio da função
» dominio função
» Domínio da função
» Domínio da função!
PiR2 :: Matemática :: Álgebra
Página 2 de 2
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
