Domínio da função

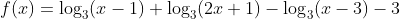Seja e 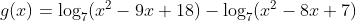. Qual o domínio da função  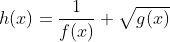em forma de intervalo?

Pietro

O que significa - 3_e ?

Problema simples para qualquer aluno do Ensino Médio:

1)Use as propriedades de logaritmos pra simplificar f(x)

2) Idem para calcular g(x), fatorando cada logaritmando

3) Seja R o radicando de g(x) ---> R >= 0. Seja L o logaritmando de g(x) ---> L > 0

4) Seja L' o logaritmando de f(x) ---> f(x) ≠ 0 e L' > 0

Vou pensar nas dicas que me deu e volto a escrever quando tiver alguma pronto.

Obrigado Elcio.

Bom dia Elcio!

Simplificando f(x) encontrei:



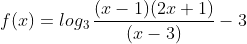
Em f(x), (x -1)(2x + 1) deve ser maior que zero.

Resolvendo o produto acima encontrei como raízes x' = 1 e x" = -1/2

No denominador --> x ≠ 3


Simplificando g(x) encontrei:




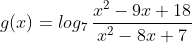
Como prosseguir?

1) Você não explicou o que 3_e

2) Sua conclusão sobre f(x) está errada: (x - 1).(2x + 1) > 0

O correto é (x- 1).(2x + 1)/(x - 3) > 0 --- Você NÃO pode deixar (x - 3) de fora!!!

Faça a tabela verdade para as três funções e descubra os intervalos onde o logaritmando é positivo.

3) Você não seguiu minhas instruções: NÃO fatorou o numerador e o denominador do logaritmando de g(x)

Após fatorar use a tabela verdade tanto para o logaritmando > 0, quanto para raiz do logaritmando >= 0 e determine os intervalos

- 3<sub>e ---> Esqueci de dar o espaço separando a função f da função g.


Posso fazer isso?


x - 1 > 0 ---> x > 1


2x + 1 > 0 ---> x > -1/2


x - 3 > 0 ---> x > 3</sub>


Os gráficos das três funções acima são positivos (com valores à esquerda de x negativos e à direita positivos).


Montando um diagrama percebi que o intervalo para as três funções acima está compreendido entre (3 , +∞).


Até aqui está certo?

Este intervalo ]3 , +∞[ está certo mas NÃO é o único

Em g(x): 

No numerador: x² - 9x + 18 >0 (Isso implica dizer que x = 6 e x = 3).

Quanto ao denominador Elcio tenho dúvidas! 

O denominador deve ser maior que zero. Quando resolvo a equação do 2° grau encontro:

x' = 7    e       x" = 1

Montando o gráfico para as equações da função g(x):

x² - 9x + 18  --> Parábola com concavidade para cima (à esquerda de 3 valores positivos e à direita de 6 valores também positivos).

A mesma ideia estou utilizando para o denominador x² - 8x +7.

Com isso, cheguei nesses dois intervalos: 

]-∞ , 3[ U (6 , +∞)


e


]-∞ , 1[ U (7 , +∞)



Até aqui está certo?

Alguém para me dizer se até aqui está correto e me dar um norte para prosseguir?

Psetro

Você está muito apressado meu caro: postou sua penúltima mensagem às 13:35 e já estava cobrando às 14:25 !!!

E você nem conseguiu ainda determinar os dois intervalos de f(x) !!!

Erros na sua mensagem:

1) "O denominador tem que ser maior que zero" ---> Errado, pois o denominador pode ser negativo.

O certo é "o denominador tem que ser diferente de zero"

2) O denominador de g(x) está errado: x² - 8x - 7 ---> O correto x² - 8x + 7 

3) Não entendi o que você quis dizer:

x² - 9x + 18  --> Parábola com concavidade para cima (à esquerda de 3 valores positivos e à direita de 6 valores também positivos).

Os seus intervalos para g(x) estão errados