Distância percorrida
2 participantes
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
 Distância percorrida
Distância percorrida
A posição de uma partícula que se desloca ao longo do eixo x varia com o tempo de acordo com a equação x = ct² - bt³, onde "x" está em metros e "t" em segundos. Suponha os valores numéricos de c e b sejam 3,0 e 2,0, respectivamente. Pergunta-se:
Qual a distância percorrida pela partícula?
No gabarito diz que que a resposta é 82m e eu encontrei -80m.
Certo de sua atenção,
Pietro di Bernadone
Qual a distância percorrida pela partícula?
No gabarito diz que que a resposta é 82m e eu encontrei -80m.
Certo de sua atenção,
Pietro di Bernadone

Pietro di Bernadone- Grupo
Velhos amigos do Fórum
- Mensagens : 1344
Data de inscrição : 04/03/2010
Idade : 34
Localização : Rio de Janeiro
 Re: Distância percorrida
Re: Distância percorrida
Pela equação, então:
x = 3t²-2t³
x = t²(3-2t)
Ou seja, as raizes da função, a posição do x equivale a zero quando:
t=0, t=0, t=3/2
Se t=0 --> x=0
Se t=0.5 --> x=0.5
Se t=1 --> x=1
Se t=1.5 --> x=0
Se t=2 --> x=-4
Se t=2.5 --> x=-12.5
Se t=3 --> x=-27
Se t=4 --> x=-80
Assim, quando t=4, então está na posição x=-80
Mas o móvel chega ao ponto x=1, e volta. Ou seja, até chegar ao ponto 1, então percorreu 1. Até voltar à origem, então x=0.
Portanto, quando ele sai, e volta, ele percorre 2 m.
E quando t=4, está na posição -80, então além dos 2 m, então ele percorre mais 80. Portanto, 82 metros percorridos.
Podemos saber que o ponto máximo é 1 pois se fizer a derivada, obteremos que o valor da derivada descreve a velocidade. Como até o ponto máximo ele possuia velocidade positiva, então no ponto máximo sua velocidade equivale a zero.
f(t) = 3t² - 2t²
f'(t) = 6t - 6t²
0 = 6t(1-t)
Ou seja, t=0, ou t=1, sua velocidade será zero. Assim, como t=1, x=1. Ou seja, sua posição máxima é 1 até inverter o sentido.
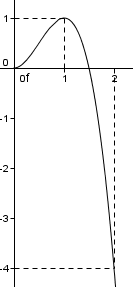
x = 3t²-2t³
x = t²(3-2t)
Ou seja, as raizes da função, a posição do x equivale a zero quando:
t=0, t=0, t=3/2
Se t=0 --> x=0
Se t=0.5 --> x=0.5
Se t=1 --> x=1
Se t=1.5 --> x=0
Se t=2 --> x=-4
Se t=2.5 --> x=-12.5
Se t=3 --> x=-27
Se t=4 --> x=-80
Assim, quando t=4, então está na posição x=-80
Mas o móvel chega ao ponto x=1, e volta. Ou seja, até chegar ao ponto 1, então percorreu 1. Até voltar à origem, então x=0.
Portanto, quando ele sai, e volta, ele percorre 2 m.
E quando t=4, está na posição -80, então além dos 2 m, então ele percorre mais 80. Portanto, 82 metros percorridos.
Podemos saber que o ponto máximo é 1 pois se fizer a derivada, obteremos que o valor da derivada descreve a velocidade. Como até o ponto máximo ele possuia velocidade positiva, então no ponto máximo sua velocidade equivale a zero.
f(t) = 3t² - 2t²
f'(t) = 6t - 6t²
0 = 6t(1-t)
Ou seja, t=0, ou t=1, sua velocidade será zero. Assim, como t=1, x=1. Ou seja, sua posição máxima é 1 até inverter o sentido.


Carlos Adir- Monitor

- Mensagens : 2820
Data de inscrição : 27/08/2014
Idade : 28
Localização : Gurupi - TO - Brasil
 Tópicos semelhantes
Tópicos semelhantes» distância percorrida
» Distância Percorrida
» Distância percorrida
» Distância Percorrida
» distância percorrida e som
» Distância Percorrida
» Distância percorrida
» Distância Percorrida
» distância percorrida e som
PiR2 :: Física :: Mecânica Geral
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












