Bissetriz do menor ângulo
4 participantes
Página 1 de 1
 Bissetriz do menor ângulo
Bissetriz do menor ângulo
A equação da bissetriz do menor ângulo formado pelas retas y = √3x + 2 e 3y = √3 x + 6 é :
Tentei resolver da seguinte maneira
Achei o ângulo entre as retas por: tgθ = |a - a'|/(1+a.a').
Achei o ponto onde as retas se encontram igualando as equações
Tentei utilizar a equação fundamental da reta através da tangente e utilizando o ponto onde as retas se cruzam
Não consegui chegar ao gabarito!!
Há algum erro na minha forma de resolver?
Obrigado desde já!
- Spoiler:
- y=x+2
Tentei resolver da seguinte maneira
Achei o ângulo entre as retas por: tgθ = |a - a'|/(1+a.a').
Achei o ponto onde as retas se encontram igualando as equações
Tentei utilizar a equação fundamental da reta através da tangente e utilizando o ponto onde as retas se cruzam
Não consegui chegar ao gabarito!!
Há algum erro na minha forma de resolver?
Obrigado desde já!
ViniciusAlmeida12- Mestre Jedi

- Mensagens : 725
Data de inscrição : 02/02/2013
Idade : 28
Localização : Bahia
 Re: Bissetriz do menor ângulo
Re: Bissetriz do menor ângulo
Para obter a eq. das bissetrizes basta igualar: d(P,r) = d(P,s) onde P é um ponto qualquer da bissetriz.
|(√3)x -y + 2|/√((√3)²+1²) = | (√3)x -3y + 6|/√((√3)² + 3²)
(√3x - y + 2)/√4 = +- (√3x -3y + 6)/√12
(√3x -y+2)(√3) = +- (√3x - 3y + 6)
3x -√3y + 2√3 = + √3x -3y + 6
(3-√3)x +(3-√3)y - 2(3-√3) = 0
x + y - 2 = 0
y = -x + 2
ou
3x - √3y + 2√3 = -√3x + 3y - 6
(3+√3)x -(3+√3)y +2(3+√3) = 0
x - y + 2 = 0
y = x+ 2 ( menor ângulo)
|(√3)x -y + 2|/√((√3)²+1²) = | (√3)x -3y + 6|/√((√3)² + 3²)
(√3x - y + 2)/√4 = +- (√3x -3y + 6)/√12
(√3x -y+2)(√3) = +- (√3x - 3y + 6)
3x -√3y + 2√3 = + √3x -3y + 6
(3-√3)x +(3-√3)y - 2(3-√3) = 0
x + y - 2 = 0
y = -x + 2
ou
3x - √3y + 2√3 = -√3x + 3y - 6
(3+√3)x -(3+√3)y +2(3+√3) = 0
x - y + 2 = 0
y = x+ 2 ( menor ângulo)

Luck- Grupo
Velhos amigos do Fórum
- Mensagens : 5322
Data de inscrição : 20/09/2009
Idade : 32
Localização : RJ
 Re: Bissetriz do menor ângulo
Re: Bissetriz do menor ângulo
Quando temos questões como essa. Onde pede-se a equação da bissetiz de duas retas, sempre teremos duas equações para a bissetriz? Se sim, essas duas bissetrizes sempre serão perpendiculares?
anabeatrizneves- Iniciante
- Mensagens : 47
Data de inscrição : 18/01/2015
Idade : 28
Localização : Alagoinhas, Bahia, Brasil
 Re: Bissetriz do menor ângulo
Re: Bissetriz do menor ângulo
Para este caso, poderia fazer assim:
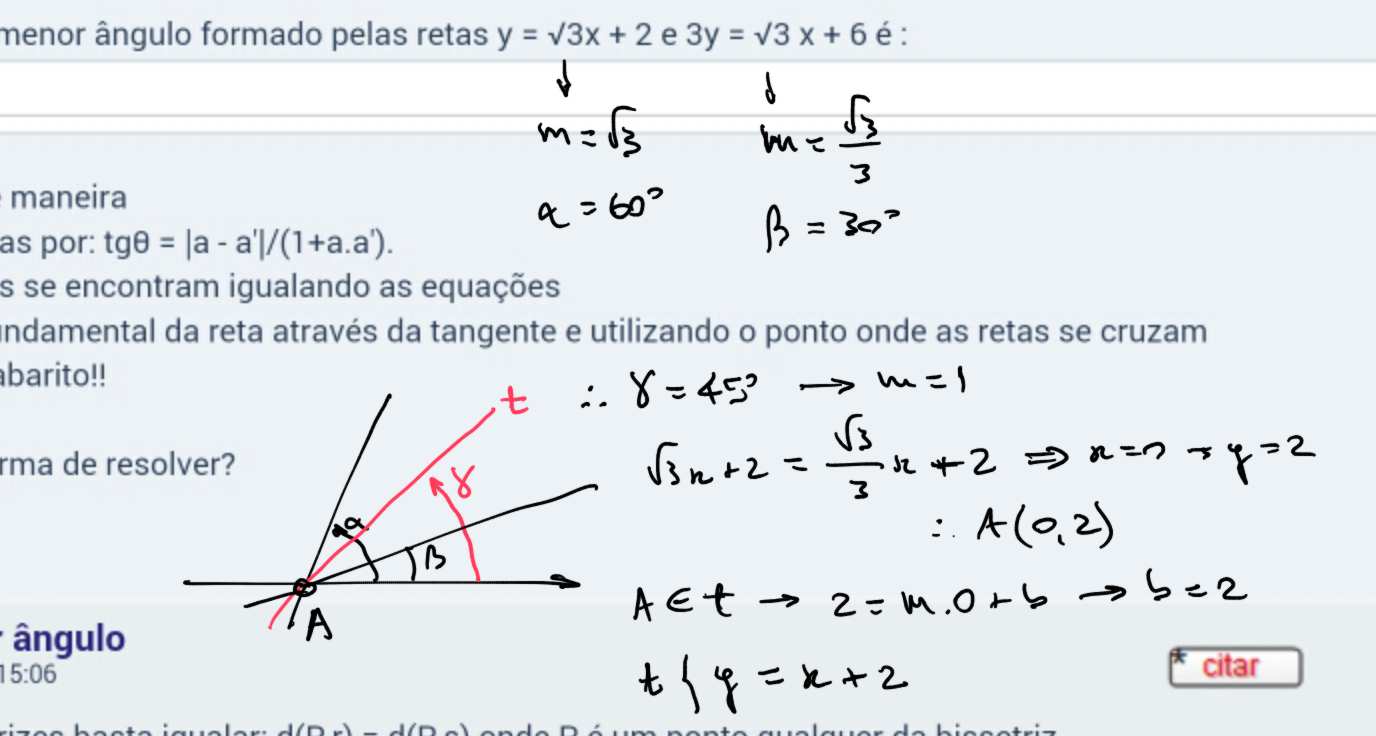


Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
anabeatrizneves- Iniciante
- Mensagens : 47
Data de inscrição : 18/01/2015
Idade : 28
Localização : Alagoinhas, Bahia, Brasil
 Re: Bissetriz do menor ângulo
Re: Bissetriz do menor ângulo
Ana Beatriz,anabeatrizneves escreveu:Quando temos questões como essa. Onde pede-se a equação da bissetiz de duas retas, sempre teremos duas equações para a bissetriz? Se sim, essas duas bissetrizes sempre serão perpendiculares?
SIM e SIM.
Sim, se temos duas retas concorrentes e não perpendiculares (caso em que o ângulo seria de 90°), elas formam dois pares de ângulos diferenfes opostos pelo vértice, um menor e o outro, consequentemente, maior. Para cada um destes dois ângulos haverá uma bissetriz e cada bissetriz pode ser descrita pela equação de uma reta.
E sim, essas duas bissetrizes são perpendiculares ente si, sempre. E nem poderia ser de outra forma pois um ângulo raso (um lado da reta) vale 180°. Se o dividimos em dois mediante corte por uma reta transversal (com o que formamos dois ângulos), e de cada um desses dois ângulos formados tomamos a metade (divisão pela bissetriz), essas metades tomadas são a metade de 180°, ou seja, 90° e as bissetrizes são perpendiculares.

Medeiros- Grupo
Velhos amigos do Fórum
- Mensagens : 10547
Data de inscrição : 01/09/2009
Idade : 72
Localização : Santos, SP, BR
 Tópicos semelhantes
Tópicos semelhantes» quação da bissetriz do menor ângulo.
» o ângulo formado pela bissetriz do ângulo interno A com a mediatriz do lado BC mede:
» Qual o ângulo descrito pela roda menor enquanto a roda maior gira de um ângulo de 12° 48' ?
» bissetriz de um angulo
» Bissetriz de um ângulo
» o ângulo formado pela bissetriz do ângulo interno A com a mediatriz do lado BC mede:
» Qual o ângulo descrito pela roda menor enquanto a roda maior gira de um ângulo de 12° 48' ?
» bissetriz de um angulo
» Bissetriz de um ângulo
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












