Prove que Raiz de X² = |X|
+7
ricardo.rad
Ashitaka
Kulo
MatheusMagnvs
Andrew Wiles
Euclides
Maxuel
11 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Página 1 de 2 • 1, 2 
 Prove que Raiz de X² = |X|
Prove que Raiz de X² = |X|
Eu sei que essa discussão já foi abordada aqui e em vários outros fóruns, ocorre que para eu assimilar e concordar com algo, não me basta guardar uma regra e sim entendê-la. Alguém poderia provar-me/explicar-me por que motivo, razão, causa ou circunstância Raiz de X² = |X| ??
Veja meu modo de pensar:
Ex:
Raiz[(-9)²] = |9| ?
Ok, pode ser => Raiz[81] = 9. Ok
Por outro lado: Raiz[(-9)²] = (-9)²/² = (-9)¹ = -9
Nessa linha re raciocínio, Raiz[(-9)²] não seria +/- 9? :scratch:
Veja meu modo de pensar:
Ex:
Raiz[(-9)²] = |9| ?
Ok, pode ser => Raiz[81] = 9. Ok
Por outro lado: Raiz[(-9)²] = (-9)²/² = (-9)¹ = -9
Nessa linha re raciocínio, Raiz[(-9)²] não seria +/- 9? :scratch:
Maxuel- Iniciante
- Mensagens : 13
Data de inscrição : 21/12/2012
Idade : 34
Localização : Minas Gerais
BRUNO F1, Nemo731BS e SrJorgensen gostam desta mensagem
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Isso, antes de mais nada, resulta da definição. A definição de raiz quadrada é tal que
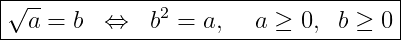
essas condições não estão colocadas aí à toa. Elas são necessárias para que não conduzam a absurdos. Admitamos que
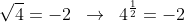
isso nos traz um primeiro problema: "como um número positivo elevado a uma potência positiva poderia fornecer um resultado negativo?"
a radiciação e a exponenciação têm uma conexão com os logaritmos
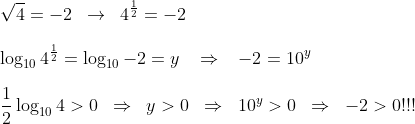
um número positivo (10), elevado a qualquer outro número (y) nunca resultará negativo. Razão de porque também não se define logaritmo de número negativo.
Enfim, em matemática, tudo que conduz a absurdos é um erro de origem, portanto
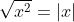
essas condições não estão colocadas aí à toa. Elas são necessárias para que não conduzam a absurdos. Admitamos que
isso nos traz um primeiro problema: "como um número positivo elevado a uma potência positiva poderia fornecer um resultado negativo?"
a radiciação e a exponenciação têm uma conexão com os logaritmos
um número positivo (10), elevado a qualquer outro número (y) nunca resultará negativo. Razão de porque também não se define logaritmo de número negativo.
Enfim, em matemática, tudo que conduz a absurdos é um erro de origem, portanto
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
victorlyra14, marcosprb, João Linhares, Arlindocampos07, Maths;-; e SrJorgensen gostam desta mensagem
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Realmente, Euclides, agora eu me convenci do certo. Obrigado pela explicação. 
Mas aproveitando a linha de raciocínio, direcionando nossa análise para uma função do 2º grau, por que, na resolução dos valores de X, a equação admite +/- para raiz do Delta?
Tipo, eu entendi a linha do raciocínio, o resultado da Raiz será um valor positivo:
Raiz(Delta) = |X|
No entanto, depois de racionado o número, a expressão admite:
[-b + Raiz(Delta)]/2a e [-b - Raiz(Delta)]/2a
Por que se faz necessário adotar tanto o valor positivo quanto o negativo do resultado da raiz para se solucionar os valores de X? :scratch:
Mas aproveitando a linha de raciocínio, direcionando nossa análise para uma função do 2º grau, por que, na resolução dos valores de X, a equação admite +/- para raiz do Delta?
Tipo, eu entendi a linha do raciocínio, o resultado da Raiz será um valor positivo:
Raiz(Delta) = |X|
No entanto, depois de racionado o número, a expressão admite:
[-b + Raiz(Delta)]/2a e [-b - Raiz(Delta)]/2a
Por que se faz necessário adotar tanto o valor positivo quanto o negativo do resultado da raiz para se solucionar os valores de X? :scratch:
Maxuel- Iniciante
- Mensagens : 13
Data de inscrição : 21/12/2012
Idade : 34
Localização : Minas Gerais
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
João Linhares gosta desta mensagem
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Ok, Euclides. Valeu mesmo pela ajuda! 
Maxuel- Iniciante
- Mensagens : 13
Data de inscrição : 21/12/2012
Idade : 34
Localização : Minas Gerais
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Ótima explicação!

Andrew Wiles- Jedi

- Mensagens : 293
Data de inscrição : 13/05/2013
Idade : 32
Localização : Belo Horizonte, Minas Gerais, Brasil.
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Gostaria de observar, sem recorrer aos logaritmos, que [(4)^1/2] = -2 é um absurdo: como 4 = 2², temos que [(4)^1/2] = [(2)²*1/2] = (2)^2/2 = 2¹ = 2.
Daí teríamos que, se [(4)^1/2] = -2, resultaria que 2 = -2, um absurdo.

MatheusMagnvs- Mestre Jedi

- Mensagens : 568
Data de inscrição : 12/11/2013
Idade : 28
Localização : Recife
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Aproveitando a dedução de Euclides, se temos
√x² = |x|
Então, por definição de módulo, temos:
x = √x² ou x = -√x²
Por isso que quando temos x² = 4, por exemplo, fazemos x = √4 ou x = -√4. Isso porque de x² = 4, fazemos:
x² = 4
√x² = √4
|x| = √4
x = √4 ou x = - √4
x = 2 ou x = -2
Além disso, se |x| = √x², √x² só pode ser maior ou igual a zero, já que o resultado de módulo nunca pode ser negativo. Com isso, já se descarta resultados como √4 = -2, por exemplo e etc.
Estou enganado?
√x² = |x|
Então, por definição de módulo, temos:
x = √x² ou x = -√x²
Por isso que quando temos x² = 4, por exemplo, fazemos x = √4 ou x = -√4. Isso porque de x² = 4, fazemos:
x² = 4
√x² = √4
|x| = √4
x = √4 ou x = - √4
x = 2 ou x = -2
Além disso, se |x| = √x², √x² só pode ser maior ou igual a zero, já que o resultado de módulo nunca pode ser negativo. Com isso, já se descarta resultados como √4 = -2, por exemplo e etc.
Estou enganado?

Kulo- Recebeu o sabre de luz

- Mensagens : 110
Data de inscrição : 18/04/2015
Idade : 29
Localização : Ceará, Brasil
swttprincess1 gosta desta mensagem
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
A verdade é que parece haver discórdia sobre a definição de raiz quadrada. Por exemplo, de uma fonte confiável: http://mathworld.wolfram.com/SquareRoot.html
temos: Note that any positive real number has two square roots, one positive and one negative.
Aplicando a definição de raiz é a dada pelo wolfram, a raiz quadrada de x é um número r tal que x = r². Dessa forma, a raiz de 16 é um número r tal que r² = 16 e, portanto, é +- 4.
Contudo, até onde sei em livros de Variáveis Complexas ou Análise Complexa há uma definição em R e outra em C, assim como é feito no Iezzi. O verdadeiro problema está no que o símbolo √ representa.
Se você pegar o Iezzi vol. 2:

Se pegar o vol. de Complexos:

Note que da primeira definição, se a = 4, b = 2, necessariamente.
Da segunda, se a = 4, b = 2 ou b = -2.
Observe também a sutileza das definições: a primeira é chamada de raiz enésima artimética enquanto a segunda é chamda só de raiz.
Assim, a resposta de √4 dependerá de qual conjunto está sendo considerado, R ou C. Como o costume é sempre trabalhar em R e, nos exercícios, C - R fica renegado a exercícios específicos do assunto, resta escrever que √4 = 2, pois provavelmente é a intenção de quem perguntou (e que não dirá raiz artimética).
temos: Note that any positive real number has two square roots, one positive and one negative.
Aplicando a definição de raiz é a dada pelo wolfram, a raiz quadrada de x é um número r tal que x = r². Dessa forma, a raiz de 16 é um número r tal que r² = 16 e, portanto, é +- 4.
Contudo, até onde sei em livros de Variáveis Complexas ou Análise Complexa há uma definição em R e outra em C, assim como é feito no Iezzi. O verdadeiro problema está no que o símbolo √ representa.
Se você pegar o Iezzi vol. 2:

Se pegar o vol. de Complexos:

Note que da primeira definição, se a = 4, b = 2, necessariamente.
Da segunda, se a = 4, b = 2 ou b = -2.
Observe também a sutileza das definições: a primeira é chamada de raiz enésima artimética enquanto a segunda é chamda só de raiz.
Assim, a resposta de √4 dependerá de qual conjunto está sendo considerado, R ou C. Como o costume é sempre trabalhar em R e, nos exercícios, C - R fica renegado a exercícios específicos do assunto, resta escrever que √4 = 2, pois provavelmente é a intenção de quem perguntou (e que não dirá raiz artimética).

Ashitaka- Monitor

- Mensagens : 4365
Data de inscrição : 12/03/2013
Localização : São Paulo
 Re: Prove que Raiz de X² = |X|
Re: Prove que Raiz de X² = |X|
Bem explicado, agora ficou claro depois de ver esses argumentos.

ricardo.rad- Iniciante
- Mensagens : 40
Data de inscrição : 26/06/2016
Idade : 25
Localização : Parnaíba,Piauí
Página 1 de 2 • 1, 2 
 Tópicos semelhantes
Tópicos semelhantes» Raiz dentro de raiz, tendendo ao infinito
» Prove se n não for Q.P,entao raiz de N é IR
» Algoritmos para raiz quadrada e raiz enésima (por: Elcioschin)
» Equação Logaritima, problema de uma raiz com indice em raiz
» [Resolvido]Raiz dentro de raiz
» Prove se n não for Q.P,entao raiz de N é IR
» Algoritmos para raiz quadrada e raiz enésima (por: Elcioschin)
» Equação Logaritima, problema de uma raiz com indice em raiz
» [Resolvido]Raiz dentro de raiz
PiR2 :: Matemática :: Álgebra
Página 1 de 2
Permissões neste sub-fórum
Não podes responder a tópicos












