Fórmula de Heaviside(decomposição em frações
2 participantes
Página 1 de 1
Fórmula de Heaviside(decomposição em frações
por Matheus Fillipe Sex 07 Mar 2014, 21:08
Pra quem já estuda transformada de Laplace ou até mesmo integrais que requerem a decomposição em frações parciais, ta ai um método realmente prático. Requer o uso da derivada de primeira ordem e funciona para divisões de polinômios da forma:
}{Q(x)} "\frac{P(x)}{Q(x)}")
Condições:
1ºSendo a tal que Q(a)=0 deveremos ter Q'(a) diferente de 0, para todos os a possíveis.
2º O grau de P menor que o de Q.
Com as duas condições podemos aplicar o método.
Demonstração:
Se Q é um polinômio com N zeros distintos, temos que como o de costume com frações parciais:
}{Q(x)}=\sum_{n=1}^{N}\frac{A_n}{x-a_n} "\frac{P(x)}{Q(x)}=\sum_{n=1}^{N}\frac{A_n}{x-a_n}")
Ou seja, a soma de todos os coeficientes A para determinar(note que há 1 para cada raiz) considerando Q na forma:
=(x-a_1)(x-a_2)(x-a_3)...(x-a_N)=\prod_{n=0}^{N}(x-a_n) "Q(x)=(x-a_1)(x-a_2)(x-a_3)...(x-a_N)=\prod_{n=0}^{N}(x-a_n)")
Agora vem os passos decisivos: Multiplicando ambos os lados por
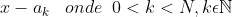
Temos:
}{Q(x)}(x-a_k)=\frac{A_1&space;(x-a_k)}{x-a_1}+...A_k...\frac{A_N(x-a_k)}{x-a_N} "\frac{P(x)}{Q(x)}(x-a_k)=\frac{A_1 (x-a_k)}{x-a_1}+...A_k...\frac{A_N(x-a_k)}{x-a_N}")
Nossa intenção é achar o Ak ali no meio. Ficaria fácil se tomássemos x=ak, mas com isso o termo P/Q tenderia a infinito/não faria sentido. Assim tomaremos o limite de X-->ak. A intenção é que se os termos multiplicados por (x-ak) se anulem mais rapidamente que o polinômio, pois o x-ak que multiplica a fração se cancela com o que está em Q, no denominador. Vejamos, aplicando Le'Hoptal a esse limite:
}{Q(x)}(x-a_k)=P(a_k)\lim_{x->a_k}\frac{(x-a_k)}{Q(x)} "A_k=\lim_{x->a_k}\frac{P(x)}{Q(x)}(x-a_k)=P(a_k)\lim_{x->a_k}\frac{(x-a_k)}{Q(x)}")
Se você observar verá que o termo:
}{Q(x)} "\lim_{x->a_k}\frac{(x-a_k)}{Q(x)}")
É o inverso de:
}{(x-a_k)}=&space;\lim_{x->a_k}\frac{Q(x)}{\delta&space;x}=\frac{\mathrm{d}&space;Q(x)}{\mathrm{d}&space;x}|_{x=a_k}=Q'(a_k) "\lim_{x->a_k}\frac{Q(x)}{(x-a_k)}= \lim_{x->a_k}\frac{Q(x)}{\delta x}=\frac{\mathrm{d} Q(x)}{\mathrm{d} x}|_{x=a_k}=Q'(a_k)")
Portanto chegamos a:
}{Q'(a_k)} "A_k=\frac{P(a_k)}{Q'(a_k)}")
e:
}{Q(x)}=\sum_{n=1}^{N}\frac{P(a_n)}{Q'(a_n)(x-a_n)} "\frac{P(x)}{Q(x)}=\sum_{n=1}^{N}\frac{P(a_n)}{Q'(a_n)(x-a_n)}")
Que és chamada de Fórmula do Desenvolvimento de Heaviside.
Pode aparacer complicado a primeira vista, vejamos um exemplo fácil e um real:
(x-3))} "\frac{2x^2-4}{(x+1(x-2)(x-3))}")
As raízes são explicitamente -1,2,3. P(-1)=-2 ; p(2)=4 ; P(3)=14.
Agora, Q'=3x^2 -8x+1. Q'(-1)=3+8+1=12, Q'(2)=12-16+1=-3;Q'(3)=27-24+1=4
Portanto:
(x-2)(x-3)}=\frac{-2}{12(x+1)}+\frac{4}{-3(x-2)}+\frac{14}{4(x-3)} "\frac{2x^2-4}{(x+1)(x-2)(x-3)}=\frac{-2}{12(x+1)}+\frac{4}{-3(x-2)}+\frac{14}{4(x-3)}")
Agora um bom exemplo:
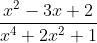
Fatorando:
P=x^2-3x+2=(x-2)(x-1) só pra facilitar
Q=x^4+2x^2+1=(x^2+1)(x^2+1) necessariamente
Q'=3x^3 +4x
as raízes são duplas, -i e i, portanto:
P(-i)=1+3i Q'(-i)=-3i-4i=-7i
p(i)=1-3i Q'(i)=i
você encontraria:
(x+i)}-\frac{i+3}{(x-i)} "-\frac{1+3i}{(7i)(x+i)}-\frac{i+3}{(x-i)}")
O método só será útil quando for possível encontrar as raízes de Q.
Espero que gostem, Obrigado!
Condições:
1ºSendo a tal que Q(a)=0 deveremos ter Q'(a) diferente de 0, para todos os a possíveis.
2º O grau de P menor que o de Q.
Com as duas condições podemos aplicar o método.
Demonstração:
Se Q é um polinômio com N zeros distintos, temos que como o de costume com frações parciais:
Ou seja, a soma de todos os coeficientes A para determinar(note que há 1 para cada raiz) considerando Q na forma:
Agora vem os passos decisivos: Multiplicando ambos os lados por
Temos:
Nossa intenção é achar o Ak ali no meio. Ficaria fácil se tomássemos x=ak, mas com isso o termo P/Q tenderia a infinito/não faria sentido. Assim tomaremos o limite de X-->ak. A intenção é que se os termos multiplicados por (x-ak) se anulem mais rapidamente que o polinômio, pois o x-ak que multiplica a fração se cancela com o que está em Q, no denominador. Vejamos, aplicando Le'Hoptal a esse limite:
Se você observar verá que o termo:
É o inverso de:
Portanto chegamos a:
e:
Que és chamada de Fórmula do Desenvolvimento de Heaviside.
Pode aparacer complicado a primeira vista, vejamos um exemplo fácil e um real:
As raízes são explicitamente -1,2,3. P(-1)=-2 ; p(2)=4 ; P(3)=14.
Agora, Q'=3x^2 -8x+1. Q'(-1)=3+8+1=12, Q'(2)=12-16+1=-3;Q'(3)=27-24+1=4
Portanto:
Agora um bom exemplo:
Fatorando:
P=x^2-3x+2=(x-2)(x-1) só pra facilitar
Q=x^4+2x^2+1=(x^2+1)(x^2+1) necessariamente
Q'=3x^3 +4x
as raízes são duplas, -i e i, portanto:
P(-i)=1+3i Q'(-i)=-3i-4i=-7i
p(i)=1-3i Q'(i)=i
você encontraria:
O método só será útil quando for possível encontrar as raízes de Q.
Espero que gostem, Obrigado!
Matheus Fillipe- Mestre Jedi
- Mensagens : 893
Data de inscrição : 19/05/2013
Idade : 26
Localização : Araxá
Re: Fórmula de Heaviside(decomposição em frações
por Man Utd Sáb 08 Mar 2014, 14:13
Olá 
Achei interessante esse metódo, mas eu conheço uma versão diferente dessa fórmula : (Aqui vai o link) nesta versão ela fornece diretamente a transformada inversa de laplace.
Dúvida: se as raízes forem complexas (como seu último exemplo) , como conseguirei a transformada inversa de laplace ?
Obrigado por compartilhar, com esse metódo ganha-se muito tempo na hora de decompor em frações parciais.
Achei interessante esse metódo, mas eu conheço uma versão diferente dessa fórmula : (Aqui vai o link) nesta versão ela fornece diretamente a transformada inversa de laplace.
Dúvida: se as raízes forem complexas (como seu último exemplo) , como conseguirei a transformada inversa de laplace ?
Obrigado por compartilhar, com esse metódo ganha-se muito tempo na hora de decompor em frações parciais.
Man Utd- Grupo
Velhos amigos do Fórum
- Mensagens : 1119
Data de inscrição : 18/08/2012
Idade : 29
Localização : Manchester
Re: Fórmula de Heaviside(decomposição em frações
por Matheus Fillipe Sáb 08 Mar 2014, 22:17
Conheço o método que já dá a transformada inversa direto, e ele é totalmente baseado nisso. No último exemplo era só por mostrar mesmo, não seria possível fazer a transformada inversa por frações parciais até onde eu sei.
Matheus Fillipe- Mestre Jedi
- Mensagens : 893
Data de inscrição : 19/05/2013
Idade : 26
Localização : Araxá
Tópicos semelhantes» Transformada de Laplace+ Heaviside + Série de potência
» Como escrevo a fórmula da queda livre a partir do repouso e a fórmula do lançamento vertical para baixo?
» Frações com frações algébricas [Resolvido]
» Decomposição
» Decomposição
» Como escrevo a fórmula da queda livre a partir do repouso e a fórmula do lançamento vertical para baixo?
» Frações com frações algébricas [Resolvido]
» Decomposição
» Decomposição
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos|
|
|
