Numeros complexos e sistemas

por PedroCunha Seg 03 Mar 2014, 02:59

Olá, amigos.

Se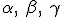 $Numeros complexos e sistemas Mimetex$ são números complexos tais que :

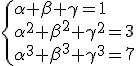
$Numeros complexos e sistemas Mimetex$

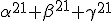
Determine o valor de $Numeros complexos e sistemas Mimetex$

Bom, consegui resolver o exercício. A resolução é a seguinte:

$\\\\ S_3 = \sigma_1^3 - 3\sigma_1 \sigma_2 + 3\sigma_3 \therefore 7 = 1 - 3 \cdot 1 \cdot (-1) + 3 \sigma_3 \therefore \sigma_3 = 1 \\\\ S_4 = \sigma_1 \cdot S_3 - \sigma_2 \cdot S_2 + \sigma_3 \cdot S_1 \therefore S_4 = 7 +3 + 1 \therefore S_4 = 11 \rightarrow S_4 = S_1 + S_2 + S_3 \\ S_5 = \sigma_1 \cdot S_4 - \sigma_2 \cdot S_3 + \sigma_3 \cdot S_2 \therefore S_5 = 11 + 7 + 3 \therefore S_5 = 21 \rightarrow S_5 = S_2 + S_3 + S_4 \\\\\circ S_6 = S_5 + S_4 + S_3 \therefore S_6 = 39 \\ \circ S_7 = S_6 + S_5 + S_4 \therefore S_7 = 71 \\ \circ S_8 = 131 \\ \circ S_9 = 241 \\ \circ S_{10} = 443 \\ \circ S_{11} = 815 \\ \circ S_{12} = 1499 \\ \circ S_{13} =2757 \\ \circ S_{14} = 5071 \\ \circ S_{15} = 9327 \\ \circ S_{16} = 17155 \\ \circ S_{17} = 31553 \\ \circ S_{18} = 58035 \\ \circ S_{19} = 106743 \\ \circ S_{20} = 196331 \\ \Leftrightarrow S_{21} = 361109$

Para resolver, utilizei as Somas de Newton (Polinômios Simétricos). A minha dúvida é a seguinte:

Como deduzir, sabendo que cada soma é igual à soma das três somas anteriores, a expressão que representa a soma pedida (no caso,S_{21}) ?

Tentei descobrir, mas cheguei em uma recorrência gigante e não consegui sair do lugar. Vejam:

S_{21} = S_{20} + S_{19} + S_{18} .:. (S_{19} + S_{18} + S_{17}) + (S_{18} +S_{17} + S_{16}) + (S_{17} + S_{16} + S_{15})

e assim por diante.

Ou será que a única maneira de chegar no resultado final é no 'braço' mesmo?

Obrigado pela atenção.

Abraços,
Pedro

por Luck Seg 03 Mar 2014, 22:27

Acho que sim, essa recorrência não forma uma soma telescópica. 'Braço' mesmo seria tentar resolver isso sem utilizar polinômios simétricos Smile

.

por PedroCunha Seg 03 Mar 2014, 22:29

Hahaha. Falou tudo, Luck.

À princípio tentei buscar alguma coisa no campo dos complexos, tendo em vista que utilizando a primeira Lei de Moivre, supostamente seria mais fácil. No entanto, não consegui sair do lugar.

Abraços,
Pedro

por Conteúdo patrocinado

Numeros complexos e sistemas

Numeros complexos e sistemas

Re: Numeros complexos e sistemas

Re: Numeros complexos e sistemas

Re: Numeros complexos e sistemas

Um fórum livre e democrático.