Imagem de uma função
3 participantes
PiR2 :: Matemática :: Álgebra
Página 1 de 1
 Imagem de uma função
Imagem de uma função
Determine o conjunto imagem da função:
f(x)=x²-x+1/x²+x+1
Resposta: 1/3 ≤ f(x) ≤ 3
Alguém poderia me dar uma força?
f(x)=x²-x+1/x²+x+1
Resposta: 1/3 ≤ f(x) ≤ 3
Alguém poderia me dar uma força?
victorheiji- Iniciante
- Mensagens : 31
Data de inscrição : 11/04/2013
Idade : 29
Localização : São Paulo, São Paulo , Brasil
 Re: Imagem de uma função
Re: Imagem de uma função
O conjunto imagem de f(x) é igual ao domínio da inversa de f(x). Calculando agora fˉ¹(x):
y=(x²-x+1)/(x²+x+1)
x²y+xy+y=x²-x+1
x²(y-1)+x(y+1)+(y-1)=0
x={-y-1±√[(y+1)²-4(y-1)²]}/2(y-1)
fˉ¹(x)={-x-1±√[(x+1)²-4(x-1)²]}/2(x-1)
i) x-1≠0 ⇒ x≠1
ii) (x+1)²-4(x-1)²≥0 ⇒ 3x²-10x+3≤0 ⇒ 1/3≤x≤3
Como i) está contido em ii), o domínio da inversa de f(x) é 1/3≤x≤3. Logo, a imagem de f(x) é 1/3≤f(x)≤3.
até
y=(x²-x+1)/(x²+x+1)
x²y+xy+y=x²-x+1
x²(y-1)+x(y+1)+(y-1)=0
x={-y-1±√[(y+1)²-4(y-1)²]}/2(y-1)
fˉ¹(x)={-x-1±√[(x+1)²-4(x-1)²]}/2(x-1)
i) x-1≠0 ⇒ x≠1
ii) (x+1)²-4(x-1)²≥0 ⇒ 3x²-10x+3≤0 ⇒ 1/3≤x≤3
Como i) está contido em ii), o domínio da inversa de f(x) é 1/3≤x≤3. Logo, a imagem de f(x) é 1/3≤f(x)≤3.
até

Igor Bragaia- Jedi

- Mensagens : 400
Data de inscrição : 24/10/2012
Idade : 27
Localização : Piracicaba, SP, Brasil
 Re: Imagem de uma função
Re: Imagem de uma função
Acho que o desejado é exatamente o que fez muito bem o colega Igor Bragaia. Porém, se conhecermos derivação e limites, teremos outro caminho:
=\frac{2x^2-2}{x^4+2x^3+3x^2+2x+1})
a derivada se anula em dois pontos: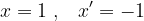
um deles poderá ser um ponto de máximo global e o outro um ponto de mínimo global. Uma verificação decisiva poderá ser feita pelo exame dos limites laterais
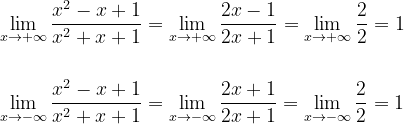
os limites mostram que há uma assíntota horizontal em y=1. Assim podemos decidir sobre o máximo e o mínimo
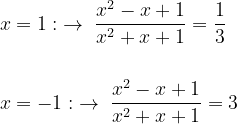
portanto\leq&space;3)
a derivada se anula em dois pontos:
um deles poderá ser um ponto de máximo global e o outro um ponto de mínimo global. Uma verificação decisiva poderá ser feita pelo exame dos limites laterais
os limites mostram que há uma assíntota horizontal em y=1. Assim podemos decidir sobre o máximo e o mínimo
portanto
____________________________________________
In memoriam - Euclides faleceu na madrugada do dia 3 de Abril de 2018.

Lembre-se de que os vestibulares têm provas de Português também! Habitue-se a escrever corretamente em qualquer circunstância!
O Universo das coisas que eu não sei é incomensuravelmente maior do que o pacotinho de coisas que eu penso que sei.

Euclides- Fundador

- Mensagens : 32508
Data de inscrição : 07/07/2009
Idade : 74
Localização : São Paulo - SP
 Re: Imagem de uma função
Re: Imagem de uma função
Fantástico vocês, me ajudaram demais!!! Eu estava que nem louco tentando fatorar a expressão para tentar deixá-la em função de apenas uma expressão quadrática, mas não estava saindo. Muito obrigado mesmo pela ajuda!
victorheiji- Iniciante
- Mensagens : 31
Data de inscrição : 11/04/2013
Idade : 29
Localização : São Paulo, São Paulo , Brasil
PiR2 :: Matemática :: Álgebra
Página 1 de 1
Permissões neste sub-fórum
Não podes responder a tópicos












