Binômio de Newton.

Sabendo que o desenvolvimento de {2x²-[2/(3x)]}^n possui 7 termos e que um deles é 240ax^6, acharemos para "a" o valor:
a) 4/9
b) 2/9 
c) 1/9
d) 2/3
e) 5/3


Gabarito: letra A. 
Se puderem detalhar a resolução dessa questão e deixar claro cada passo, agradeço. Tive muita dificuldade em resolvê-la. 

Como no desenvolvimento do binômio há 7 termos, n=6, pois, como sabemos, cada termo do desenvolvimento de (a+b)^n tem a forma 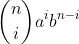, para todo i de 0 à n ( e de 0 à n temos n+1 números, certo?)

Ok, já sabemos que n=6, e esse é o maior problema.

Podemos achar. agora, qual(is) dos termos terá x^6. Felizmente, nosso binômio é pequeno, e na pior das hipóteses poderiamos desenvolver tudo.

Mas veja se você concorda: Os termos com x^6 são os termos em que i são maiores (4 pra frente, olhe para o i do nosso termo geral), pois o expoente de (2x^2) deve ser grande o suficiente para "cancelar" com o de 3x no denominador de -2/3x. 

Podemos também verificar que i tem que ser par, pois, como o valor de a nas alternativas é positivo, o expoente ao qual (-2/3x) foi elevado é par. Vamos analisar nossas alternativas para usar ao nosso favor  Podeos notar que se i=6, o expoente do x será 12. Só nos resta i=4.

Então vejamos:

Para i = 4:


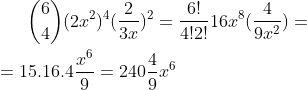
Veja se ficou bem explicado. Se não entender, me avise que eu explico de novo, certo?

Só vou pedir par colocar a questão, da próxima vez, no lugar correto. Binômio não é matéria do ensino fundamental.

Abraços

Só ficou confuso a parte em que acabou em 15.16.4/9x^6, como vou resolver a multiplicação de 16x^8 . 4/9x^2?

Divisão de potências de mesma base: Mantém a base e subtrai-se os expoente.

Step-by-step:



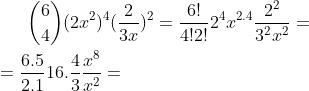
Se não entender ainda, avise

por qual motivo o "i" deve ser maior que 4 ?? o i poderia ser 2 também!!

por qual motivo o "i" deve ser maior que 4 ?? o i poderia ser 2 também!!