IMO (Olimpíada In. de Mate.) - 1959 - Q. 1

por Convidado Qui 14 Fev 2013, 14:06

Relembrando a primeira mensagem :

ORIGINAL;
01. Prove that the fraction $\frac{21n+4}{14n+3}$ is irreducible for every natural number n.

TRADUÇÃO LIVRE;
01. Prove que a fração $\frac{21n+4}{14n+3}$ é irredutível para cada número natural n.

Já agradeço. Só para informar, estou sem o gabarito.

por felipesantos Sex 15 Fev 2013, 22:12

olá caro parofi, o seu exemplo não se enquadra na questão acima , e considero a solução do mauk03 brilhante, a minha solução e do luck estão certíssimas . Não podemos esquecer que estamos nos tratando com uma questão de olimpíada internacional ,logo pode haver várias soluções , dependendo da criatividade intelectual do aluno!!

Valeu e abraço!!

por Convidado Sex 15 Fev 2013, 22:25

Valeu pelos comentários. Sobre o "Algoritmo de Euclides", por curiosidade, isso está presente em "Os Elementos" (livro do "Pai da Geometria" - Euclides)? (Caso alguém saiba)

por felipesantos Sex 15 Fev 2013, 22:52

Sim, sim é verdade faz parte da obra "Elementos de Euclides", o mais legal que o grande Euclides via o algoritmo por interpretação geométrica.
Muito show! cheers

por felipesantos Sáb 16 Fev 2013, 15:43

Olá pessoal achei mas uma solução, observem :
Seja (p/q)= é uma fracão irredutível de modo que o mdc(p,q)=1.
Vamos lá:

(21n+4)/(14n+3 )= (p/q) → q(21n+4)=p(14n+3) → 21nq - 14np = 3p - 4p →

n(21q-14p)=3p-4q → n= (3p-4q)/(21q-14p) .

Agora analisando ; n ∈ ℕ ⇒ 21q-14p ≠ 0 (p/q)≠ (21/14),
primeira parte provada .

Agora a segunda parte 3p-4q ≥ 0 → (p/q) ≥ 4/3 ,todos esses valores maiores 4/3 , só vale para o mdc(p,q)=1 .

C.Q.D

por carlosalmeida57 Sáb 30 Jan 2021, 20:18

Prova de fração irredutível / IMO 1959-#1
=========================================
Neste vídeo é detalhada a metodologia adequada para demonstrar a iredutibilidade de uma fração.
São apresentados 3 métodos:
► 1º método: análise de intervalos de variação e teste de hipóteses
(método apresentado apenas como indicação de inviável para a demonstração)
► 2º método: corolário do Teorema de Bezout
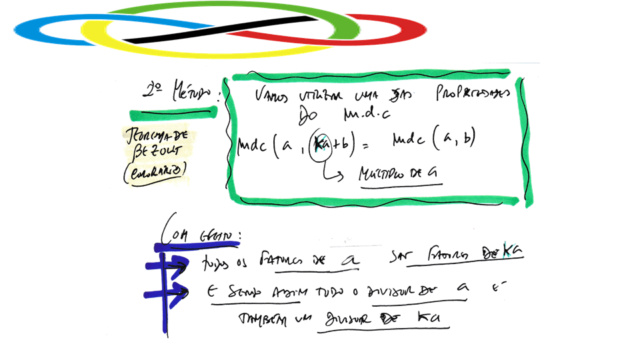
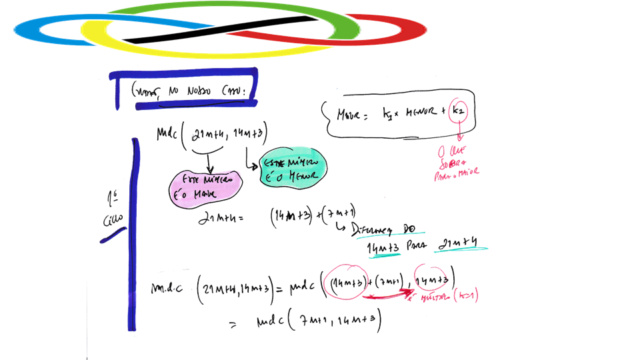
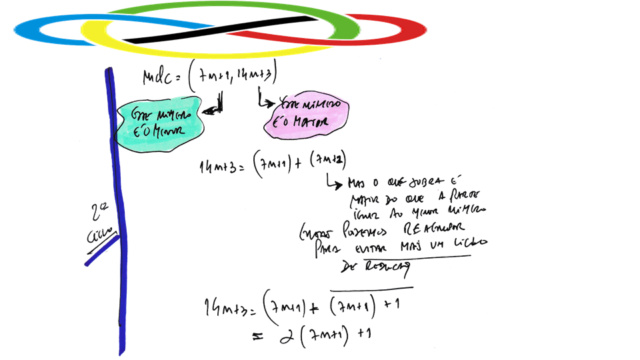
► 3º método: propriedade do m.d.c. decorrente do algoritmo de Euclides

Link do vídeo: https://youtu.be/SP5IbF13b7k