Desafio - MHS - 1

por duduzao Sáb 26 Jan 2013, 15:29

Quanto tempo dura o choque entre uma bola de futebol de raio r e massa m, em uma parede ?
Dados: pressão interna = p
Pressão atmosférica = p0

não tenho gabarito.

por **Euclides** Sáb 26 Jan 2013, 19:55

OBS: trata-se de uma tentativa da qual não estou totalmente seguro.

No choque a bola se deforma até que receba da parede uma pressão que somada à pressão atmosférica iguale a pressão interna. Vou supor que a área de aplicação dessa força seja a secção transversal da bola.

$\frac{F}{S}+P_0=P\;\;\to\;\;F=S(P-P_0)$

O impulso recebido é igual à variação do momento linear, em módulo temos

$F.t=2mv\;\to\;\;t=\frac{2mv}{S(P-P_0)}=\frac{2mv}{\pi r^2(P-P_0)}$

por duduzao Sáb 26 Jan 2013, 22:20

Euclides,
Na área, não devemos utilizar 4pir² ?

por **Euclides** Sáb 26 Jan 2013, 22:39

duduzao escreveu:Euclides,
Na área, não devemos utilizar 4pir² ?

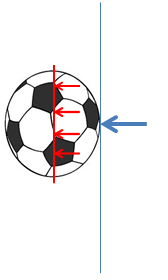
Não há como considerar que a força aplicada pela parede envolva a bola. Eis como considerei:

Desafio - MHS - 1 Bola-1_zps194b78cf

por **Mimetist** Dom 19 Abr 2015, 20:58

Suponha que, durante o choque, a bola adquira uma elongação x.

Analisemos como varia a pressão interna do gás durante o choque, assumindo que tenhamos uma transformação isotérmica:

\frac{4p_{1}\pi r^3}{3}=p\Big(\frac{4\pi r^3}{3}-\frac{\pi x^2(3r-x)}{3}\Big) \iff p=\frac{4p_{1}r^3}{4r^3-x^2(3r-x)} \ \ \ (II)

Reescrevendo (II) :

p=\frac{4p_{1}r^3}{4r^3-x^2(3r-x)}=\frac{p_{1}}{1-\frac{x^2(3r-x)}{4r^3}}

x << r \ \ \ \rightarrow \ \ p \approx p_{1}

Com a condição imposta acima, a pressão interna é aproximadamente constante, assim, basta compararmos as pressões externa e interna.

Considere que a área onde a força é aplicada seja a área de uma calota esférica, portanto:

\Delta p=p-p_{o}=\frac{F}{2\pi rx} \ \iff \ F=2\pi r(p-p_{o})x=kx

Assim:

k=2\pi r(p-p_{o}) \ \ \ \ (III)

Do movimento harmônico simples:

\omega=\frac{2\pi}{T}=\sqrt{\frac{k}{m}} \ \ \ (IV)

(III) \ \ \ \text{em} \ \ \ (IV) :

\frac{2\pi}{T}=\sqrt{\frac{2\pi r(p-p_{o})}{m}} \ \ \iff T=2\pi \sqrt{\frac{m}{2\pi r(p-p_{o})}}

O tempo de choque, t_{c}, corresponde à metade de uma oscilação do sistema, ou seja:

t_{c}=\frac{T}{2}

Portanto:

\boxed{t_{c}=\pi\sqrt{\frac{m}{2\pi r(p-p_{o})}}} \ \ \ \text{ou} \ \ \ \ \boxed{t_{c}=\sqrt{\frac{\pi m}{2 r(p-p_{o})}}}