Matrizes

Um computador atribui um número inteiro diferente a cada caractere do teclado. Para transmitir uma mensagem pela internet, esta é transformada em uma sequência de números inteiros consecutivos que é codificada do seguinte modo: A cada grupo de 4
caracteres consecutivos a, b, c, d, o computador
multiplica a matriz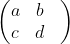
) à direita pela matriz (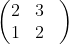
) e
transmite o resultado (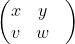
) na sequência x, y, v, w.


Por exemplo, a sequência 1, 8, 11, 3 é transmitida como a sequência 10, 19, 25, 39. Então,

(A) O receptor da sequência 10, 19, 25, 39 não pode
decodificar exatamente qual foi a sequência original
enviada.
(B) O receptor só pode identificar sequências de
caracteres de 4 números inteiros desde que sejam
menores que 64.
(C) Se o receptor recebe a sequência 8, 15, 29, 36,
então, a soma dos 4 números transmitidos é 17, mas
não se sabe quais são estes números.
(D) Se o receptor recebe a sequência 8, 15, 29, 36,
então, a soma dos 4 números transmitidos é 25, e
pode-se saber exatamente quais são estes números.
(E) Quaisquer sequência de 4 números, dentro das
capacidades computacionais dos equipamentos,
poderá ser decodificada sem ambiguidades.


GABARITO (E)

Obrigado desde já

Multiplicando as matrizes chegamos aos seguintes sistemas:
2a + b = x
3a + 2b = y

2c + d = v
3c + 2d = w

Note que ambos os sistemas sao possiveis e determinados e portanto não vão existir ambiguidades e nem valores que não possam ser decodificados.
De cara, letra E.