Propriedades de matrizes e operações com matrizes UFSC

por dedepensando Qua 05 Jan 2022, 15:48

Exercício UFSC
Determine verdadeiro ou falso:

Proposição 08.
Se A;B;C são matrizes inversíveis, então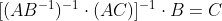 $Propriedades de matrizes e operações com matrizes UFSC Gif$

A resolução da proposição mostra o seguinte:

Propriedades de matrizes e operações com matrizes UFSC 1QSUOERGLUkCLiFiUAlpExKIU0CIiFqWAFhGxKE0NFcuy2Wra5LiqpZkcNZ8CWixJwSOiEoeIiGUpoEVELEoBLSJiUQpoERGLUkCLiFiUAlpExKIU0CIiFqWAFhGxKAW0iIhFKaBFRCxKAS0iYlEKaBERi1JAi4hYlAJaRMSiFNAiIhalgBYRsSgFtIiIRSmgRUQsSgEtImJRCmgREYtSQIuIWJQCWkTEov4PmmNsX4Vmb1UAAAAASUVORK5CYII=

Porém, não consigo entender quais propriedades de matrizes que foram utilizadas para simplificar a equação e chegar na resposta.

por **qedpetrich** Qua 05 Jan 2022, 16:04

Olá dedepensando;

Realmente ficou um pouco confuso, pois detalharam o que não precisava na minha opinião.

Uma maneira mais direta:

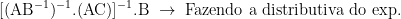
$Propriedades de matrizes e operações com matrizes UFSC Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7B%5B%28AB%5E%7B-1%7D%29%5E%7B-1%7D.%28AC%29%5D%5E%7B-1%7D.B%20%5C%20%5Crightarrow%20%5C%20Fazendo%20%5C%20a%20%5C%20distributiva%20%5C%20do%20%5C%20exp$

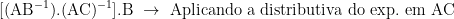
$Propriedades de matrizes e operações com matrizes UFSC Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7B%5B%28AB%5E%7B-1%7D%29.%28AC%29%5E%7B-1%7D%5D.B%20%5C%20%5Crightarrow%20%5C%20Aplicando%20%5C%20a%20%5C%20distributiva%20%5C%20do%20%5C%20exp$

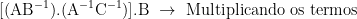
$Propriedades de matrizes e operações com matrizes UFSC Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7B%5B%28AB%5E%7B-1%7D%29.%28A%5E%7B-1%7DC%5E%7B-1%7D%29%5D$

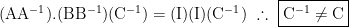
$Propriedades de matrizes e operações com matrizes UFSC Png.latex?%5Cdpi%7B100%7D%20%5Cmathrm%7B%28AA%5E%7B-1%7D%29$

por **Rory Gilmore** Qua 05 Jan 2022, 16:11

I) O inverso de um produto de matrizes inversíveis é o produto das inversas em ordem oposta:
(A.B-1)^-1 = B.A^-1

Logo:
[(A.B-1)^-1.(A.C)]^-1.B = [B.A^-1.(A.C)]^-1.B

II) O produto de uma matriz pela sua inversa é a matriz identidade:
A^-1.A = I

Então:
[B.A^-1.(A.C)]^-1.B = [B.C]^-1.B

III) Pelo mesmo motivo de I, vem:
[B.C]^-1 = C^-1B^-1

Assim:
[B.C]^-1.B = C^-1B^-1.B

IV) Por fim, temos:
C^-1B^-1.B = C^-1 que é diferente de C em geral.

Obs.: na resposta que você trouxe foi usada uma notação errada, o inverso de uma matriz não é 1 sobre a matriz. E tem outros erros na resposta apresentada.

por **qedpetrich** Qua 05 Jan 2022, 16:17

Se baseie na resposta do(a) Rory, está mais concreta!

por dedepensando Qua 05 Jan 2022, 19:46

Rory Gilmore escreveu:I) O inverso de um produto de matrizes inversíveis é o produto das inversas em ordem oposta:
(A.B-1)^-1 = B.A^-1

Logo:
[(A.B-1)^-1.(A.C)]^-1.B = [B.A^-1.(A.C)]^-1.B

II) O produto de uma matriz pela sua inversa é a matriz identidade:
A^-1.A = I

Então:
[B.A^-1.(A.C)]^-1.B = [B.C]^-1.B

III) Pelo mesmo motivo de I, vem:
[B.C]^-1 = C^-1B^-1

Assim:
[B.C]^-1.B = C^-1B^-1.B

IV) Por fim, temos:
C^-1B^-1.B = C^-1 que é diferente de C em geral.

Olá Rory! Obrigado pela resposta, esclareceu várias de minhas dúvidas!

No passo:
"Então:
[B.A^-1.(A.C)]^-1.B = [B.C]^-1.B"

O parêntese que envolve A.C pôde ser ignorado em "[B.A^-1.(A.C)]" seguindo a propriedade associativa "(A.B).C = A.(B.C)" da multiplicação de matrizes, certo?
Dessa forma, você multiplicou A^-1pelo A localizado dentro de "(A.C)", obtendo assim uma matriz identidade "[B.I.C]^-1 = [B.C]^-1", certo?

Outra pergunta que tenho, a distributiva dos expoentes não podem ser realizadas como em uma operação numérica (exemplo:
Propriedades de matrizes e operações com matrizes UFSC EqWZb8R5SWIwCktB2JynIkKJfDC1RqO2RZsookcxRtq0KWJRLjx9IjqRwfu+1IGMiyxANx57gOtiNhIMsSD8Sdo2hbFbIsIYiQrOXPIYjHDYmSkA4SJSEdJEpCOkiUhHT8C+b6KSw2aQLqAAAAAElFTkSuQmCC

Propriedades de matrizes e operações com matrizes UFSC EqWZb8R5SWIwCktB2JynIkKJfDC1RqO2RZsookcxRtq0KWJRLjx9IjqRwfu+1IGMiyxANx57gOtiNhIMsSD8Sdo2hbFbIsIYiQrOXPIYjHDYmSkA4SJSEdJEpCOkiUhHT8C+b6KSw2aQLqAAAAAElFTkSuQmCC

), mas sim apenas seguindo a propriedade I de sua explicação, correto?

por **Rory Gilmore** Qua 05 Jan 2022, 20:35

Sim, tudo que você observou está correto.

Não vale que (A.B)^-1 seja A^-1.B^-1.

Tanto é que se buscou uma fórmula para isso e ela é justamente o que usamos para resolver a questão (A.B)^-1 = B^-1.A^-1